20.4 Waves bounded on both sides by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

20.4 Waves bounded on both sides

In the examples discussed in section 20.3, it was theoretically true that a pulse would be trapped permanently in the middle medium, but that pulse was not central to our discussion, and in any case it was weakening severely with each partial reflection. Now consider a guitar string. At its ends it is tied to the body of the instrument itself, and since the body is very massive, the behavior of the waves when they reach the end of the string can be understood in the same way as if the actual guitar string was attached on the ends to strings that were extremely massive, q. Reflections are most intense when the two media are very 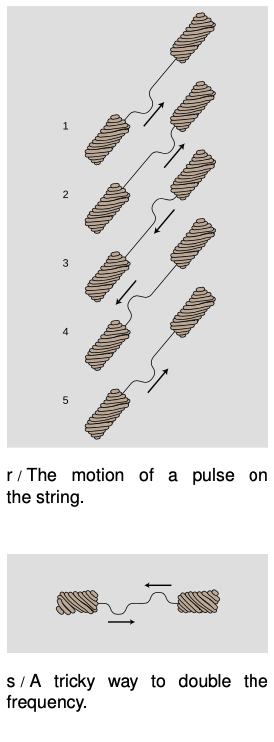dissimilar. Because the wave speed in the body is so radically different from the speed in the string, we should expect nearly `100%` reflection.

Although this may seem like a rather bizarre physical model of the actual guitar string, it already tells us something interesting about the behavior of a guitar that we would not otherwise have understood. The body, far from being a passive frame for attaching the strings to, is actually the exit path for the wave energy in the strings. With every reflection, the wave pattern on the string loses a tiny fraction of its energy, which is then conducted through the body and out into the air. (The string has too little cross-section to make sound waves efficiently by itself.) By changing the properties of the body, moreover, we should expect to have an effect on the manner in which sound escapes from the instrument. This is clearly demonstrated by the electric guitar, which has an extremely massive, solid wooden body. Here the dissimilarity between the two wave media is even more pronounced, with the result that wave energy leaks out of the string even more slowly. This is why an electric guitar with no electric pickup can hardly be heard at all, and it is also the reason why notes on an electric guitar can be sustained for longer than notes on an acoustic guitar.

If we initially create a disturbance on a guitar string, how will the reflections behave? In reality, the finger or pick will give the string a triangular shape before letting it go, and we may think of this triangular shape as a very broad “dent” in the string which will spread out in both directions. For simplicity, however, let's just imagine a wave pattern that initially consists of a single, narrow pulse traveling up the neck, r/1. After reflection from the top end, it is inverted, 3. Now something interesting happens: figure 5 is identical to figure 1. After two reflections, the pulse has been inverted twice and has changed direction twice. It is now back where it started. The motion is periodic. This is why a guitar produces sounds that have a definite sensation of pitch.

self-check E:

Notice that from r/1 to r/5, the pulse has passed by every point on the string exactly twice. This means that the total distance it has traveled equals `2L`, where `L` is the length of the string. Given this fact, what are the period and frequency of the sound it produces, expressed in terms of `L` and `v`, the velocity of the wave?

(answer in the back of the PDF version of the book)

Note that if the waves on the string obey the principle of superposition, then the velocity must be independent of amplitude, and the guitar will produce the same pitch regardless of whether it is played loudly or softly. In reality, waves on a string obey the principle of superposition approximately, but not exactly. The guitar, like just about any acoustic instrument, is a little out of tune when played loudly. (The effect is more pronounced for wind instruments than for strings, but wind players are able to compensate for it.)

Now there is only one hole in our reasoning. Suppose we somehow arrange to have an initial setup consisting of two identical pulses heading toward each other, as in figure s. They will pass through each other, undergo a single inverting reflection, and come back to a configuration in which their positions have been exactly interchanged. This means that the period of vibration is half as long. The frequency is twice as high.

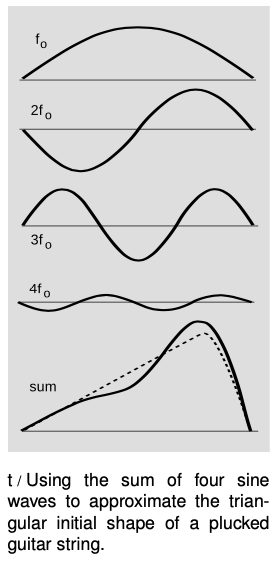
This might seem like a purely academic possibility, since nobody actually plays the guitar with two picks at once! But in fact it is an example of a very general fact about waves that are bounded on both sides. A mathematical theorem called Fourier's theorem states that any wave can be created by superposing sine waves. Figure t shows how even by using only four sine waves with appropriately chosen amplitudes, we can arrive at a sum which is a decent approximation to the realistic triangular shape of a guitar string being plucked. The one-hump wave, in which half a wavelength fits on the string, will behave like the single pulse we originally discussed. We call its frequency `f_o`. The two-hump wave, with one whole wavelength, is very much like the two-pulse example. For the reasons discussed above, its frequency is `2f_o`. Similarly, the three-hump and four-hump waves have frequencies of `3f_o` and `4f_o`.

Theoretically we would need to add together infinitely many such wave patterns to describe the initial triangular shape of the string exactly, although the amplitudes required for the very high frequency parts would be very small, and an excellent approximation could be achieved with as few as ten waves.

We thus arrive at the following very general conclusion. Whenever a wave pattern exists in a medium bounded on both sides by media in which the wave speed is very different, the motion can be broken down into the motion of a (theoretically infinite) series of sine waves, with frequencies `f_o`, `2f_o`, `3f_o`, ... Except for some technical details, to be discussed below, this analysis applies to a vast range of sound-producing systems, including the air column within the human vocal tract. Because sounds composed of this kind of pattern of frequencies are so common, our ear-brain system has evolved so as to perceive them as a single, fused sensation of tone.

Musical applications

Many musicians claim to be able to pick out by ear several of the frequencies `2f_o`, `3f_o`, ..., called overtones or harmonics of the fundamental `f_o`, but they are kidding themselves. In reality, the overtone series has two important roles in music, neither of which depends on this fictitious ability to “hear out” the individual overtones.

First, the relative strengths of the overtones is an important part of the personality of a sound, called its timbre (rhymes with “amber”). The characteristic tone of the brass instruments, for example, is a sound that starts out with a very strong harmonic series extending up to very high frequencies, but whose higher harmonics die down drastically as the attack changes to the sustained portion of the note.

Second, although the ear cannot separate the individual harmonics of a single musical tone, it is very sensitive to clashes between the overtones of notes played simultaneously, i.e., in harmony. We tend to perceive a combination of notes as being dissonant if they have overtones that are close but not the same. Roughly speaking, strong overtones whose frequencies differ by more than 1% and less than 10% cause the notes to sound dissonant. It is important to realize that the term “dissonance” is not a negative one in music. No matter how long you search the radio dial, you will never hear more than three seconds of music without at least one dissonant combination of notes. Dissonance is a necessary ingredient in the creation of a musical cycle of tension and release. Musically knowledgeable people don't use the word “dissonant” as a criticism of music, although dissonance can be used in a clumsy way, or without providing any contrast between dissonance and consonance.

Standing waves

Figure v shows sinusoidal wave patterns made by shaking a rope. I used to enjoy doing this at the bank with the pens on chains, back in the days when people actually went to the bank. You might think that I and the person in the photos had to practice for a long time in order to get such nice sine waves. In fact, a sine wave is the only shape that can create this kind of wave pattern, called a standing wave, which simply vibrates back and forth in one place without moving. The sine wave just creates itself automatically when you find the right frequency, because no other shape is possible.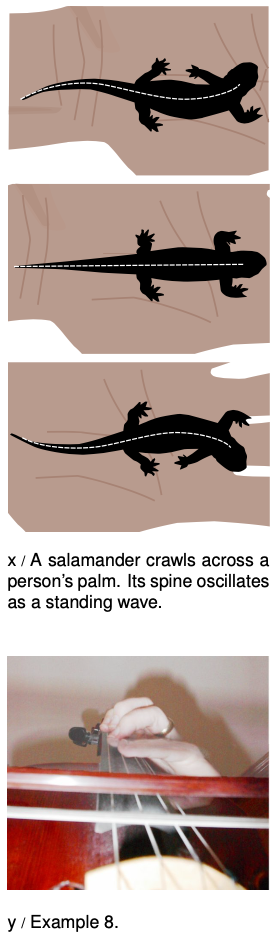

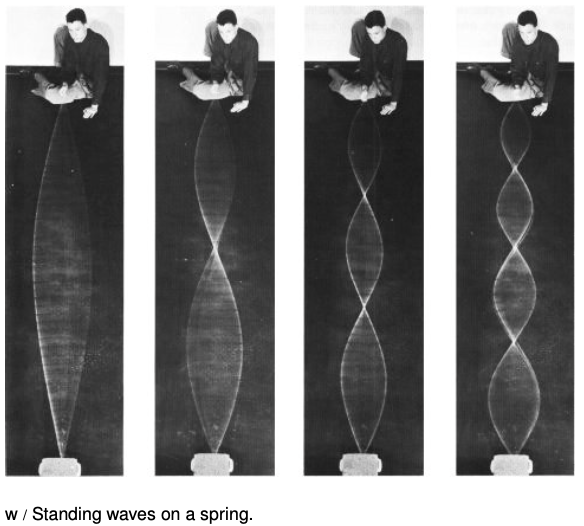
If you think about it, it's not even obvious that sine waves should be able to do this trick. After all, waves are supposed to travel at a set speed, aren't they? The speed isn't supposed to be zero! Well, we can actually think of a standing wavhttps://www.vcalc.com/wiki/lm-bounded-wavese as a superposition of a moving sine wave with its own reflection, which is moving the opposite way. Sine waves have the unique mathematical property, w, that the sum of sine waves of equal wavelength is simply a new sine wave with the same wavelength. As the two sine waves go back and forth, they always cancel perfectly at the ends, and their sum appears to stand still.

Standing wave patterns are rather important, since atoms are really standing-wave patterns of electron waves. You are a standing wave!

Example 8: Harmonics on string instruments

Figure x shows a violist playing what string players refer to as a natural harmonic. The term “harmonic” is used here in a somewhat different sense than in physics. The musician's pinkie is pressing very lightly against the string --- not hard enough to make it touch the fingerboard --- at a point precisely at the center of the string's length. As shown in the diagram, this allows the string to vibrate at frequencies `2f_o,4f_o,6f_o,...`, which have stationary points at the center of the string, but not at the odd multiples `f_o,3f_o,...`. Since all the overtones are multiples of `2f_o`, the ear perceives `2f_o` as the basic frequency of the note. In musical terms, doubling the frequency corresponds to raising the pitch by an octave. The technique can be used in order to make it easier to play high notes in rapid passages, or for its own sake, because of the change in timbre.

Standing-wave patterns of air columns

The air column inside a wind instrument behaves very much like the wave-on-a-string example we've been concentrating on so far, the main difference being that we may have either inverting or noninverting reflections at the ends.

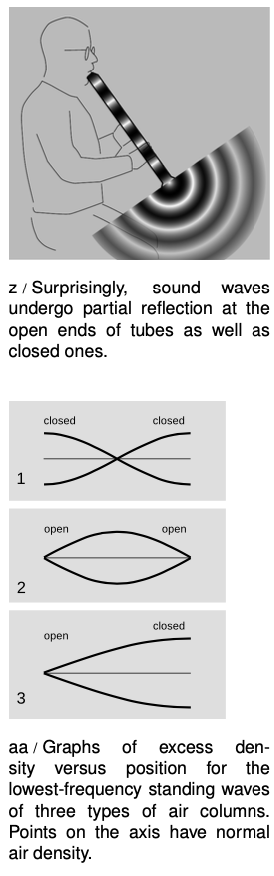
Some organ pipes are closed at both ends. The speed of sound is different in metal than in air, so there is a strong reflection at the closed ends, and we can have standing waves. These reflections are both density-noninverting, so we get symmetric standing-wave patterns, such as the one shown in figure z/1.

Figure y shows the sound waves in and around a bamboo Japanese flute called a shakuhachi, which is open at both ends of the air column. We can only have a standing wave pattern if there are reflections at the ends, but that is very counterintuitive --- why is there any reflection at all, if the sound wave is free to emerge into open space, and there is no change in medium? Recall the reason why we got reflections at a change in medium: because the wavelength changes, so the wave has to readjust itself from one pattern to another, and the only way it can do that without developing a kink is if there is a reflection. Something similar is happening here. The only difference is that the wave is adjusting from being a plane wave to being a spherical wave. The reflections at the open ends are density-inverting, z/2, so the wave pattern is pinched off at the ends. Comparing panels 1 and 2 of the figure, we see that although the wave pattens are different, in both cases the wavelength is the same: in the lowest-frequency standing wave, half a wavelength fits inside the tube. Thus, it isn't necessary to memorize which type of reflection is inverting and which is inverting. It's only necessary to know that the tubes are symmetric.

Finally, we can have an asymmetric tube: closed at one end and open at the other. A common example is the pan pipes, aa, which are closed at the bottom and open at the top. The standing wave with the lowest frequency is therefore one in which 1/4 of a wavelength fits along the length of the tube, as shown in figure z/3.

Sometimes an instrument's physical appearance can be misleading. A concert flute, ab, is closed at the mouth end and open at the other, so we would expect it to behave like an asymmetric air column; in reality, it behaves like a symmetric air column open at both ends, because the embouchure hole (the hole the player blows over) acts like an open end. The clarinet and the saxophone look similar, having a mouthpiece and reed at one end and an open end at the other, but they act different. In fact the clarinet's air column has patterns of vibration that are asymmetric, the saxophone symmetric. The discrepancy comes from the difference between the conical tube of the sax and the cylindrical tube of the clarinet. The adjustment of the wave pattern from a plane wave to a spherical wave is more gradual at the flaring bell of the saxophone.

self-check F:

Draw a graph of density versus position for the first overtone of the air column in a tube open at one end and closed at the other. This will be the next-to-longest possible wavelength that allows for a point of maximum vibration at one end and a point of no vibration at the other. How many times shorter will its wavelength be compared to the wavelength of the lowest-frequency standing wave, shown in the figure? Based on this, how many times greater will its frequency be?

(answer in the back of the PDF version of the book)

20.4 Waves bounded on both sides by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.