18.3 Putting energy into vibrations by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

18.3 Putting energy into vibrations

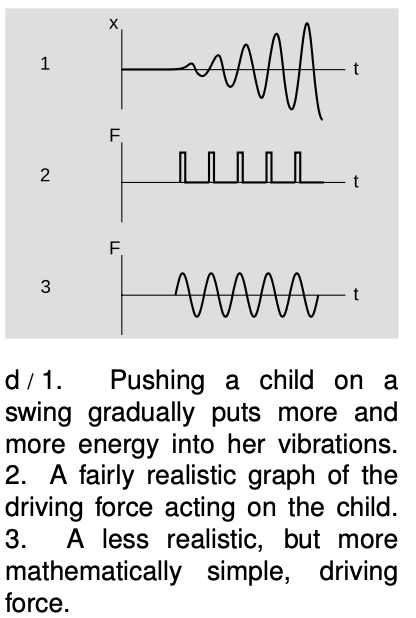When pushing a child on a swing, you cannot just apply a constant force. A constant force will move the swing out to a certain angle, but will not allow the swing to start swinging. Nor can you give short pushes at randomly chosen times. That type of random pushing would increase the child's kinetic energy whenever you happened to be pushing in the same direction as her motion, but it would reduce her energy when your pushing happened to be in the opposite direction compared to her motion. To make her build up her energy, you need to make your pushes rhythmic, pushing at the same point in each cycle. In other words, your force needs to form a repeating pattern with the same frequency as the normal frequency of vibration of the swing. Graph d/1 shows what the child's `x-t` graph would look like as you gradually put more and more energy into her vibrations. A graph of your force versus time would probably look something like graph 2. It turns out, however, that it is much simpler mathematically to consider a vibration with energy being pumped into it by a driving force that is itself a sine-wave, 3. A good example of this is your eardrum being driven by the force of a sound wave.

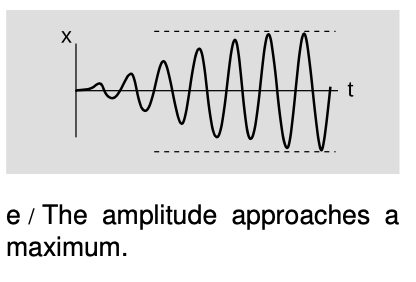Now we know realistically that the child on the swing will not keep increasing her energy forever, nor does your eardrum end up exploding because a continuing sound wave keeps pumping more and more energy into it. In any realistic system, there is energy going out as well as in. As the vibrations increase in amplitude, there is an increase in the amount of energy taken away by damping with each cycle. This occurs for two reasons. Work equals force times distance (or, more accurately, the area under the force-distance curve). As the amplitude of the vibrations increases, the damping force is being applied over a longer distance. Furthermore, the damping force usually increases with velocity (we usually assume for simplicity that it is proportional to velocity), and this also serves to increase the rate at which damping forces remove energy as the amplitude increases. Eventually (and small children and our eardrums are thankful for this!), the amplitude approaches a maximum value, `e`, at which energy is removed by the damping force just as quickly as it is being put in by the driving force.

This process of approaching a maximum amplitude happens extremely quickly in many cases, e.g., the ear or a radio receiver, and we don't even notice that it took a millisecond or a microsecond for the vibrations to “build up steam.” We are therefore mainly interested in predicting the behavior of the system once it has had enough time to reach essentially its maximum amplitude. This is known as the steady-state behavior of a vibrating system.

Now comes the interesting part: what happens if the frequency of the driving force is mismatched to the frequency at which the system would naturally vibrate on its own? We all know that a radio station doesn't have to be tuned in exactly, although there is only a small range over which a given station can be received. The designers of the radio had to make the range fairly small to make it possible to eliminate unwanted stations that happened to be nearby in frequency, but it couldn't be too small or you wouldn't be able to adjust the knob accurately enough. (Even a digital radio can be tuned to `88.0` MHz and still bring in a station at `88.1` MHz.) The ear also has some natural frequency of vibration, but in this case the range of frequencies to which it can respond is quite broad. Evolution has made the ear's frequency response as broad as possible because it was to our ancestors' advantage to be able to hear everything from a low roar to a high-pitched shriek.

The remainder of this section develops four important facts about the response of a system to a driving force whose frequency is not necessarily the same as the system's natural frequency of vibration. The style is approximate and intuitive, but proofs are given in section 18.4.

First, although we know the ear has a frequency - about 4000 Hz -  at which it would vibrate naturally, it does not vibrate at 4000 Hz in response to a low-pitched 200 Hz tone. It always responds at the frequency at which it is driven. Otherwise all pitches would sound like 4000 Hz to us. This is a general fact about driven vibrations:

Now let's think about the amplitude of the steady-state response. Imagine that a child on a swing has a natural frequency of vibration of `1` Hz, but we are going to try to make her swing back and forth at `3` Hz. We intuitively realize that quite a large force would be needed to achieve an amplitude of even `30 cm`, i.e., the amplitude is less in proportion to the force. When we push at the natural frequency of `1` Hz, we are essentially just pumping energy back into the system to compensate for the loss of energy due to the damping (friction) force. At `3` Hz, however, we are not just counteracting friction. We are also providing an extra force to make the child's momentum reverse itself more rapidly than it would if gravity and the tension in the chain were the only forces acting. It is as if we are artificially increasing the `k` of the swing, but this is wasted effort because we spend just as much time decelerating the child (taking energy out of the system) as accelerating her (putting energy in).

Now imagine the case in which we drive the child at a very low frequency, say `0.02` Hz or about one vibration per minute. We are essentially just holding the child in position while very slowly walking back and forth. Again we intuitively recognize that the amplitude will be very small in proportion to our driving force. Imagine how hard it would be to hold the child at our own head-level when she is at the end of her swing! As in the too-fast `3` Hz case, we are spending most of our effort in artificially changing the `k` of the swing, but now rather than reinforcing the gravity and tension forces we are working against them, effectively reducing `k`. Only a very small part of our force goes into counteracting friction, and the rest is used in repetitively putting potential energy in on the upswing and taking it back out on the downswing, without any long-term gain.

We can now generalize to make the following statement, which is true for all driven vibrations:

Example 5: An opera singer breaking a wine glass

In order to break a wineglass by singing, an opera singer must first tap the glass to find its natural frequency of vibration, and then sing the same note back.

Example 6: Collapse of the Nimitz Freeway in an earthquake

I led off the chapter with the dramatic collapse of the Tacoma Narrows Bridge, mainly because it was well documented by a local physics professor, and an unknown person made a movie of the collapse. The collapse of a section of the Nimitz Freeway in Oakland, CA, during a 1989 earthquake is however a simpler example to analyze.

An earthquake consists of many low-frequency vibrations that occur simultaneously, which is why it sounds like a rumble of indeterminate pitch rather than a low hum. The frequencies that we can hear are not even the strongest ones; most of the energy is in the form of vibrations in the range of frequencies from about `1` Hz to `10` Hz.

Now all the structures we build are resting on geological layers of dirt, mud, sand, or rock. When an earthquake wave comes along, the topmost layer acts like a system with a certain natural frequency of vibration, sort of like a cube of jello on a plate being shaken from side to side. The resonant frequency of the layer depends on how stiff it is and also on how deep it is. The ill-fated section of the Nimitz freeway was built on a layer of mud, and analysis by geologist Susan E. Hough of the U.S. Geological Survey shows that the mud layer's resonance was centered on about `2.5` Hz, and had a width covering a range from about `1` Hz to `4` Hz.

When the earthquake wave came along with its mixture of frequencies, the mud responded strongly to those that were close to its own natural `2.5` Hz frequency. Unfortunately, an engineering analysis after the quake showed that the overpass itself had a resonant frequency of `2.5` Hz as well! The mud responded strongly to the earthquake waves with frequencies close to `2.5` Hz, and the bridge responded strongly to the `2.5` Hz vibrations of the mud, causing sections of it to collapse.

Example 7: Collapse of the Tacoma Narrows Bridge

Let's now examine the more conceptually difficult case of the Tacoma Narrows Bridge. The surprise here is that the wind was steady. If the wind was blowing at constant velocity, why did it shake the bridge back and forth? The answer is a little complicated. Based on film footage and after-the-fact wind tunnel experiments, it appears that two different mechanisms were involved.

The first mechanism was the one responsible for the initial, relatively weak vibrations, and it involved resonance. As the wind moved over the bridge, it began acting like a kite or an airplane wing. As shown in the figure, it established swirling patterns of air flow around itself, of the kind that you can see in a moving cloud of smoke. As one of these swirls moved off of the bridge, there was an abrupt change in air pressure, which resulted in an up or down force on the bridge. We see something similar when a flag flaps in the wind, except that the flag's surface is usually vertical. This back-and-forth sequence of forces is exactly the kind of periodic driving force that would excite a resonance. The faster the wind, the more quickly the swirls would get across the bridge, and the higher the frequency of the driving force would be. At just the right velocity, the frequency would be the right one to excite the resonance. The wind-tunnel models, however, show that the pattern of vibration of the bridge excited by this mechanism would have been a different one than the one that finally destroyed the bridge.

The bridge was probably destroyed by a different mechanism, in which its vibrations at its own natural frequency of `0.2` Hz set up an alternating pattern of wind gusts in the air immediately around it, which then increased the amplitude of the bridge's vibrations. This vicious cycle fed upon itself, increasing the amplitude of the vibrations until the bridge finally collapsed.

As long as we're on the subject of collapsing bridges, it is worth bringing up the reports of bridges falling down when soldiers marching over them happened to step in rhythm with the bridge's natural frequency of oscillation. This is supposed to have happened in 1831 in Manchester, England, and again in 1849 in Anjou, France. Many modern engineers and scientists, however, are suspicious of the analysis of these reports. It is possible that the collapses had more to do with poor construction and overloading than with resonance. The Nimitz Freeway and Tacoma Narrows Bridge are far better documented, and occurred in an era when engineers' abilities to analyze the vibrations of a complex structure were much more advanced.

Example 8: Emission and absorption of light waves by atoms

In a very thin gas, the atoms are sufficiently far apart that they can act as individual vibrating systems. Although the vibrations are of a very strange and abstract type described by the theory of quantum mechanics, they nevertheless obey the same basic rules as ordinary mechanical vibrations. When a thin gas made of a certain element is heated, it emits light waves with certain specific frequencies, which are like a fingerprint of that element. As with all other vibrations, these atomic vibrations respond most strongly to a driving force that matches their own natural frequency. Thus if we have a relatively cold gas with light waves of various frequencies passing through it, the gas will absorb light at precisely those frequencies at which it would emit light if heated.

This is fairly intuitive. The steady-state behavior is an equilibrium between energy input from the driving force and energy loss due to damping. A low-`Q` oscillator, i.e., one with strong damping, dumps its energy faster, resulting in lower-amplitude steady-state motion.

self-check:

If an opera singer is shopping for a wine glass that she can impress her friends by breaking, what should she look for?

(answer in the back of the PDF version of the book)

Example 9: Piano strings ringing in sympathy with a sung note

`=>`  A sufficiently loud musical note sung near a piano with the lid raised can cause the corresponding strings in the piano to vibrate. (A piano has a set of three strings for each note, all struck by the same hammer.) Why would this trick be unlikely to work with a violin?

`=>`  If you have heard the sound of a violin being plucked (the pizzicato effect), you know that the note dies away very quickly. In other words, a violin's `Q` is much lower than a piano's. This means that its resonances are much weaker in 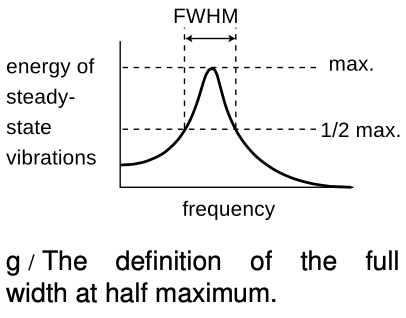amplitude.

Our fourth and final fact about resonance is perhaps the most surprising. It gives us a way to determine numerically how wide a range of driving frequencies will produce a strong response. As shown in the graph, resonances do not suddenly fall off to zero outside a certain frequency range. It is usual to describe the width of a resonance by its full width at half-maximum (FWHM) as illustrated in figure g.

Why? It is not immediately obvious that there should be any logical relationship between `Q` and the FWHM. Here's the idea. As we have seen already, the reason why the response of an oscillator is smaller away from resonance is that much of the driving force is being used to make the system act as if it had a different `k`. Roughly speaking, the half-maximum points on the graph correspond to the places where the amount of the driving force being wasted in this way is the same as the amount of driving force being used productively to replace the energy being dumped out by the damping force. If the damping force is strong, then a large amount of force is needed to counteract it, and we can waste quite a bit of driving force on changing `k` before it becomes comparable to the damping force. If, on the other hand, the damping force is weak, then even a small amount of force being wasted on changing `k` will become significant in proportion, and we cannot get very far from the resonant frequency before the two are comparable.

Example 10: Changing the pitch of a wind instrument

`=>`  A saxophone player normally selects which note to play by choosing a certain fingering, which gives the saxophone a certain resonant frequency. The musician can also, however, change the pitch significantly by altering the tightness of her lips. This corresponds to driving the horn slightly off of resonance. If the pitch can be altered by about `5%` up or down (about one musical half-step) without too much effort, roughly what is the `Q` of a saxophone?

`=>`  Five percent is the width on one side of the resonance, so the full width is about `10%`, `FWHM "/" f_(res)=0.1`. This implies a `Q` of about 10, i.e., once the musician stops blowing, the horn will continue sounding for about 10 cycles before its energy falls off by a factor of 535. (Blues and jazz saxophone players will typically choose a mouthpiece that has a low `Q`, so that they can produce the bluesy pitch-slides typical of their style. “Legit,” i.e., classically oriented players, use a higher-`Q` setup because their style only calls for enough pitch variation to produce a vibrato.)

Example 11: Decay of a saxophone tone

`=>`  If a typical saxophone setup has a `Q` of about 10, how long will it take for a 100 Hz tone played on a baritone saxophone to die down by a factor of 535 in energy, after the player suddenly stops blowing?

`=>`  A `Q` of 10 means that it takes 10 cycles for the vibrations to die down in energy by a factor of 535. Ten cycles at a frequency of 100 Hz would correspond to a time of 0.1 seconds, which is not very long. This is why a saxophone note doesn't “ring” like a note played on a piano or an electric guitar.

Example 12: `Q` of a radio receiver

`=>`  A radio receiver used in the FM band needs to be tuned in to within about 0.1 MHz for signals at about 100 MHz. What is its `Q`?

`=>` `Q=f_(res)"/"FWHM=1000`. This is an extremely high `Q` compared to most mechanical systems.

Example 13: `Q` of a stereo speaker

We have already given one reason why a stereo speaker should have a low `Q`: otherwise it would continue ringing after the end of the musical note on the recording. The second reason is that we want it to be able to respond to a large range of frequencies.

Example 14: Nuclear magnetic resonance

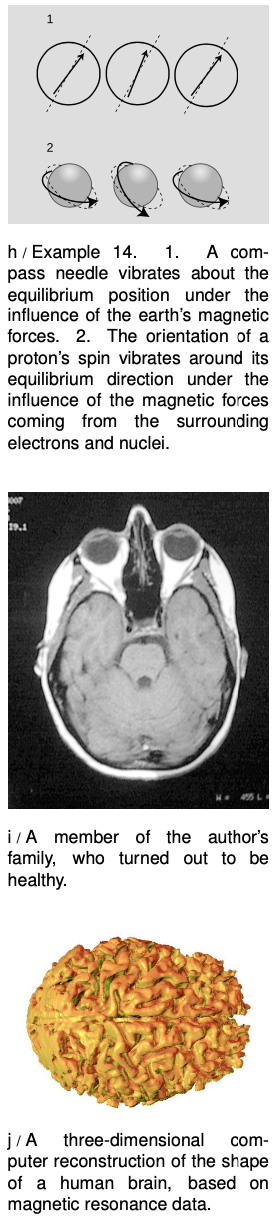
If you have ever played with a magnetic compass, you have undoubtedly noticed that if you shake it, it takes some time to settle down, h/1. As it settles down, it acts like a damped oscillator of the type we have been discussing. The compass needle is simply a small magnet, and the planet earth is a big magnet. The magnetic forces between them tend to bring the needle to an equilibrium position in which it lines up with the planet-earth-magnet.

Essentially the same physics lies behind the technique called Nuclear Magnetic Resonance (NMR). NMR is a technique used to deduce the molecular structure of unknown chemical substances, and it is also used for making medical images of the inside of people's bodies. If you ever have an NMR scan, they will actually tell you you are undergoing “magnetic resonance imaging” or “MRI,” because people are scared of the word “nuclear.” In fact, the nuclei being referred to are simply the non-radioactive nuclei of atoms found naturally in your body.

Here's how NMR works. Your body contains large numbers of hydrogen atoms, each consisting of a small, lightweight electron orbiting around a large, heavy proton. That is, the nucleus of a hydrogen atom is just one proton. A proton is always spinning on its own axis, and the combination of its spin and its electrical charge causes it to behave like a tiny magnet. The principle is identical to that of an electromagnet, which consists of a coil of wire through which electrical charges pass; the circling motion of the charges in the coil of wire makes it magnetic, and in the same way, the circling motion of the proton's charge makes it magnetic.

Now a proton in one of your body's hydrogen atoms finds itself surrounded by many other whirling, electrically charged particles: its own electron, plus the electrons and nuclei of the other nearby atoms. These neighbors act like magnets, and exert magnetic forces on the proton, h/2. The `k` of the vibrating proton is simply a measure of the total strength of these magnetic forces. Depending on the structure of the molecule in which the hydrogen atom finds itself, there will be a particular set of magnetic forces acting on the proton and a particular value of `k`. The NMR apparatus bombards the sample with radio waves, and if the frequency of the radio waves matches the resonant frequency of the proton, the proton will absorb radio-wave energy strongly and oscillate wildly. Its vibrations are damped not by friction, because there is no friction inside an atom, but by the reemission of radio waves.

By working backward through this chain of reasoning, one can determine the geometric arrangement of the hydrogen atom's neighboring atoms. It is also possible to locate atoms in space, allowing medical images to be made.

Finally, it should be noted that the behavior of the proton cannot be described entirely correctly by Newtonian physics. Its vibrations are of the strange and spooky kind described by the laws of quantum mechanics. It is impressive, however, that the few simple ideas we have learned about resonance can still be applied successfully to describe many aspects of this exotic system.

Discussion Question

A   Nikola Tesla, one of the inventors of radio and an archetypical mad scientist, told a credulous reporter in 1912 the following story about an application of resonance. He built an electric vibrator that fit in his pocket, and attached it to one of the steel beams of a building that was under construction in New York. Although the article in which he was quoted didn't say so, he presumably claimed to have tuned it to the resonant frequency of the building. “In a few minutes, I could feel the beam trembling. Gradually the trembling increased in intensity and extended throughout the whole great mass of steel. Finally, the structure began to creak and weave, and the steelworkers came to the ground panic-stricken, believing that there had been an earthquake. ... If I had kept on ten minutes more, I could have laid that building flat in the street.” Is this physically plausible?

18.3 Putting energy into vibrations by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.