The Bernoulli's Pressure calculator uses Bernoulli's equation to compute pressure (P₁) based on the following parameters. 

INSTRUCTIONS: Choose units and enter the following:

• (V₁) Velocity at elevation one.
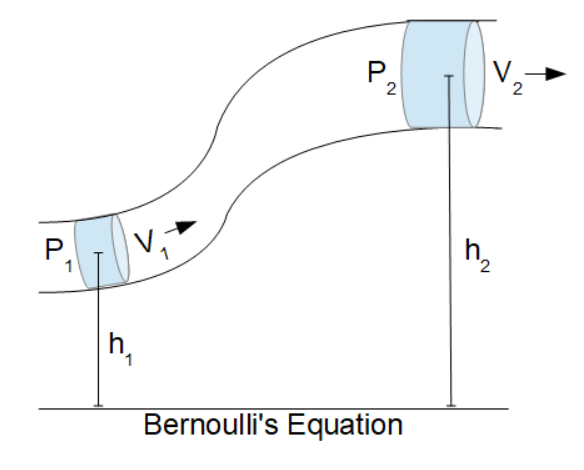
• (h₁) Height of elevation one.
• (ρ) Density of the fluid
• (P₂) Pressure at elevation two
• (V₂) Velocity at elevation two
• (h₂) Height of elevation two

Bernoulli's Pressure (P₁): The calculator returns the pressure in pascals.  However, this can be automatically converted to compatible units via the pull-down menu.

Bernoulli Equation Calculators

• Bernoulli's Pressure with any acceleration due to gravity (g)
• Bernoulli's Pressure
• Bernoulli's Velocity
• Bernoulli's Elevation

The Math / Science

Bernoulli's equation is one of the most important/useful equations in fluid mechanics. Many problems relating to real fluid are analyzed with a form of the Bernoulli equation.  

Each of the terms in the equation is expressed with units of energy per unit mass.  Note that energy per unit mass is unit equivalent to pressure.  In fluid flow, energy per unit mass is known as head.  In general, Bernoulli stated that:

1)  `P + 1/2 rho * V^2 + rho *g*h = C`    where: C is a constant.

In a combined system with two separate elevations, pressures and velocities as in the diagram above, one can make the following association:

2)  `P_1 + 1/2 rho * V_1^2 + rho *g*h_1 =  P_2 + 1/2 rho * V_2^2 + rho *g*h_2`

Based on this, the pressure at an elevation can be computed using Bernoulli's formula for pressure (P₁) and re-ordering the terms of equation 2 :

3)  `P_1 = 1/2 rho * (V_2^2 -V_1^2) + rho *g* (h_2-h_1)  + P_2`

or you can divide both sides of equation 3 by `rho *g` to get an equivalent expression for `P_1`, shown as equation 4:

4)   `P_1 = ρ*g [(V_2^2 -V_1^2)/(2*g) + (h_2-h_1)  + P_2/(ρ*g)]` 

Therefore, Bernoulli's formula for Pressure is:

          `P_1 = ρ*g [(V_2^2 -V_1^2)/(2*g) + (h_2-h_1)  + P_2/(ρ*g)]` 

where:

• P₁ is the pressure at elevation 1 based on Bernoulli's Equation
• V₁ is the velocity at elevation 1
• h₁ is the height of elevation 1
• P₂ is the pressure at elevation 2
• V₂ is the velocity at elevation 2
• h₂ is the height of elevation 2
• ρ is the density of the fluid
• g is the acceleration due to gravity

Reference

Young, Hugh and Freeman, Roger.  University Physics With Modern Physics.  Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 ) Pg 468, eq 14.17