`vecW = vecV "x" vecU `

Enter a value for all fields

The Vector Cross Product (V x U) computes the resulting vector (W) that is normal to the plane defined 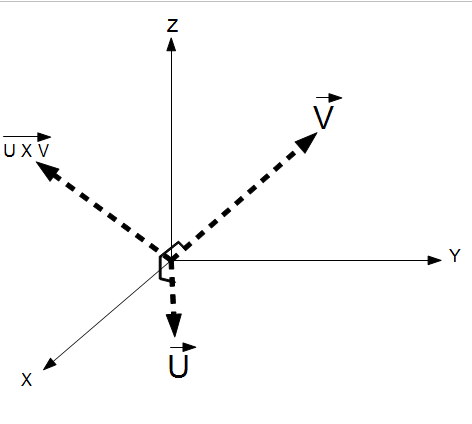 by two vectors (V and U) in three dimensional space.

INSTRUCTIONS: Enter the following:

• (V): Enter the x, y and z components of V
• (U): Enter the x, y and z components of U

Vector Cross Product (W): The calculator returns the cross product vector (e.g. 1,-2,1)

The Math / Science

The cross product of two vectors create a third vector that is orthogonal (90 degrees) from both original vectors.  This is know as a normal vector to the plane created by vectors U and V.  For this reason, a single normal vector is often used to define a plane.  To compute the cross product of two vectors, compute the determinant of the following:

                 | i        j        k |
   V x U =  |V_x     V_y     V_z|
                 |U_x    U_y     U_z|

   V x U = (V_y⋅ U_z -  U_y⋅ V_z), -1(V_x ⋅ U_z - U_x ⋅ V_z), (V_x ⋅ U_y - U_x⋅V_y)

---

3D Vector Functions

• k⋅V - scalar multiplication
• V/k - scalar division
• V / |V| - Computes the Unit Vector
• |V| - Computes the magnitude of a vector
• U + V - Vector addition
• U - V - Vector subtraction
• |U - V| - Distance between vector endpoints.
• |U + V| - Magnitude of vector sum.
• V • U - Computes the dot product of two vectors
• V x U - Computes the cross product of two vectors
• V x U • W - Computes the mixed product of three vectors
• Vector Angle - Computes the angle between two vectors
• Vector Area - Computes the area between two vectors
• Vector Projection - Compute the vector projection of V onto U.
• Vector Rotation - Compute the result vector after rotating around an axis.
• Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
• (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
• (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
• (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
• (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
• (x,y) to (r, θ) - Cartesian to Polar
• (r, θ) to (x,y) - Polar to Cartesian 
• Vector Normal to a Plane Defined by Three Points

References

• Light and Matter by Benjamin Crowell, Chapter 7.1 Vector Notation