LM 8_1 The velocity vector Collection
Tags | |
UUID | 1f5273cb-f145-11e9-8682-bc764e2038f2 |
8.1 The velocity vector by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
8.1 The velocity vector
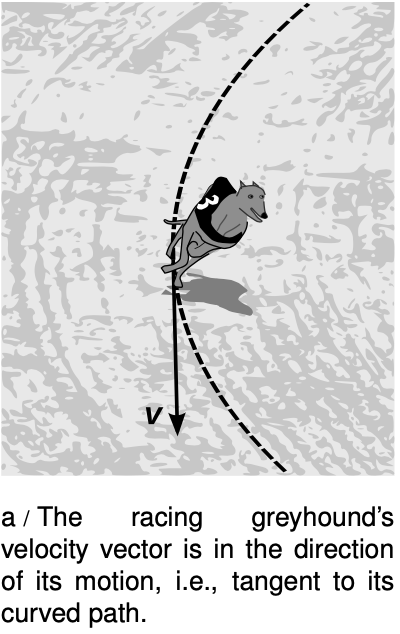 For motion with constant
velocity, the velocity vector is
For motion with constant
velocity, the velocity vector is
v = (Deltar)/(Deltat) [Only for constant velocity]
The Deltar vector points in the direction of the motion, and dividing it by the scalar Deltat only changes its length, not its direction, so the velocity vector points in the same direction as the motion. When the velocity is not constant, i.e., when the x-t, y-t, and z-t graphs are not all linear, we use the slope-of-the-tangent-line approach to define the components v_x, v_y, and v_z, from which we assemble the velocity vector. Even when the velocity vector is not constant, it still points along the direction of motion.
Vector addition is the correct way to generalize the one-dimensional concept of adding velocities in relative motion, as shown in the following example:
Example 1: Velocity vectors in relative motion
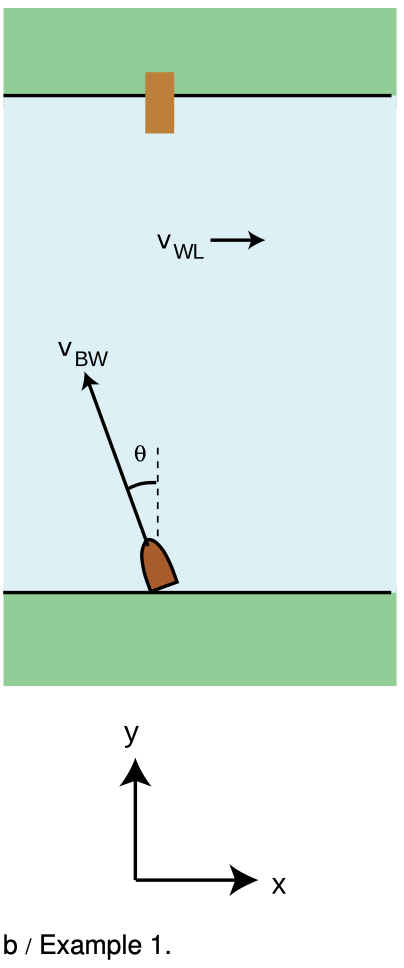 => You wish to cross a river and arrive at a dock that is directly across from you, but the river's current will tend to carry you downstream. To compensate, you must steer the boat at an angle. Find the angle theta, given the magnitude,|v_(WL)|, of the water's velocity relative to the land, and the maximum speed, |v_(BW)|, of which the boat is capable relative to the water.
=> You wish to cross a river and arrive at a dock that is directly across from you, but the river's current will tend to carry you downstream. To compensate, you must steer the boat at an angle. Find the angle theta, given the magnitude,|v_(WL)|, of the water's velocity relative to the land, and the maximum speed, |v_(BW)|, of which the boat is capable relative to the water.
=> The boat's velocity relative to the land equals the vector sum of its velocity with respect to the water and the water's velocity with respect to the land,
If the boat is to travel straight across the river, i.e., along the y axis, then we need to have v_(BL), x=0. This x component equals the sum of the x components of the other two vectors,
or
0=-|v_(BW)|sintheta+|v_(WL)|.
Solving for theta, we find
sintheta=|v_(WL)|"/"|v_(BW)|,
so
theta=sin^(-1)(|v_(WL)|/|v_(BW)|).
=> Solved problem: Annie Oakley — problem 8
Discussion Questions
mathbf"A" Is it possible for an airplane to maintain a constant velocity vector but not a constant |v|? How about the opposite - a constant |v| but not a constant velocity vector? Explain.
mathbf"B" New York and Rome are at about the same latitude, so the earth's rotation carries them both around nearly the same circle. Do the two cities have the same velocity vector (relative to the center of the earth)? If not, is there any way for two cities to have the same velocity vector?
8.1 The velocity vector by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Calculators and Collections
Equations
- Velocity - Addition KurtHeckman Use Equation
- v = (Delta r)/(Delta t) vCollections Use Equation
- River Flow Compensation pro Use Equation
- Comments
- Attachments
- Stats
No comments |
