`r = ( L )^2 / (8* "h" ) + "h" /2`

Enter a value for all fields

The Radius of a Circle based on the Chord and Arc Height calculator computes the radius based on the chord length (L) and height (h).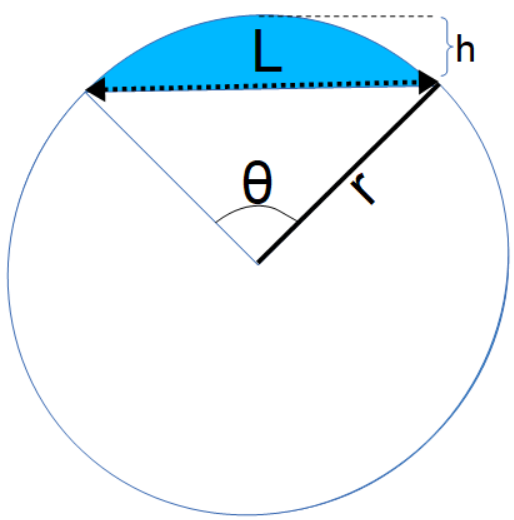

INSTRUCTIONS:  Choose units and enter the following:

• (L) Length of Chord (see diagram)
• (h) Height of Arc from the chord to the highest point.  

Radius (r): The calculator returns the radius in meters.  However, this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The formula for the radius of a circle based on the length of a chord and the height is:

  `r = L^2/(8 h) + h/2`

where:

• r is the radius of a circle
• L is the length of the chord.  This is the straight line length connecting any two points on a circle.
• h is the height above the chord.  This is the greatest distance from a point on the circle and the chord line.

A useful application of the math construct is in construction where the formulas computes the radius of an arch.

---

Circle Calculators

• Circle Area -  Computes the area of a circle given the radius (A = π r²).
• Area of Circle Arc Segment f(r,θ) - Computes the area of an arc segment of a circle given the radius (r) and angle (θ)
• Area of Circle Arc Segment Area f(r,h) - Computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
• Area of Circle Sector f(r,Θ) - Computes the area of a sector (pie slice) of a circle given the radius (r) and angle (Θ).
• Angle of Circle Sector f(r,h) - Computes the angle in a circle from the radius and depth of the chord.
• Area of Circle Annulus - Computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
• Radius of Circle from Center and a Point - Computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
• Circumference of Circle -  Computes the circumference of a circle given the radius (C = 2 π r).
• Circle Arc Length - Computes the length of an arc length on a circle given the radius (r) and angle (Θ)
• Circle within a Triangle - Computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
• Circle around a Triangle - Computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
• Circle Diameter from Area - Computes the radius and diameter of a circle from the area. 
• Circle Radius from Circumference - Computes the radius of a circle given the circumference.
• Circle Circumference from Area - Computes the circumference of a circle given the area.
• Circle Radius from Area - Computes the radius of a circle given the area.
• Chord Length: Computes the length of a chord in a circle from the radius and height.
• Circle Radius from Chord - Computes the radius of a circle based on the length of a chord and the chord's center height.
• Equation of Circle from Center and Point Coordinates - Develops the general equation of a circle based on the coordinates of the center (h,k) and any point on the circle (x,y).
• Circle with same Perimeter as an Ellipse - Computes the radius of the circle with the same perimeter of an ellipse defined by the semi-major and semi-minor axes.
• Rectangles to Cover a Circle - Computes the number of rectangles needed to minimally cover a circle based on the circle's diameter and the length and width of the rectangles.