The vector angle (2D) formula, Θ = tan-1(Δy/Δx), computes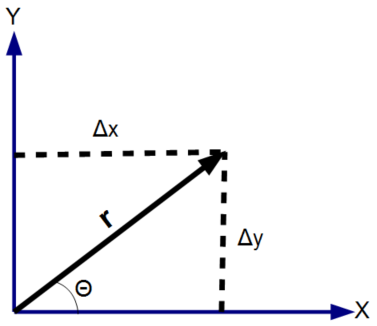
Vector r components the angle between the vector r and the x axis based on the measurement of the two components of the two dimensional vector.
INSTRUCTIONS: Enter the following:
- (Δy) y coordinate.
- (Δx) x coordinate.
vector angle (Θ): The calculator returns the angle in degree. However, this can be automatically converted to other angle units via the pull-down menu.
References
Vectors
A vector is a mathematical concept of an object that has both direction and length. A line alone is not a vector but a line with directed orientation spanning the distance between two points in space is a vector. This equation computes the component of a vector that is the vector's projection on the x-axis of Cartesian coordinates.
The Math / Science
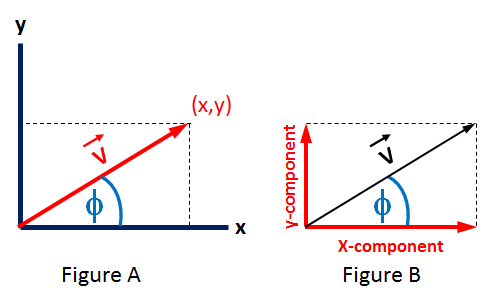
Figure A shows a vector, `bar V` (in red) represented in Cartesian coordinates. A vector can point in any direction, so there is no significance to the fact that `bar V` in Figure A is pointing to a point in the +x/+y quadrant of the Cartesian coordinates.
The direction and length of `bar V` define it as a vector and the vector can be displaced to any point in space and still be vector `bar V`. The beginning of the vector does not have to be located at the intersection of the x and y coordinates. We show vector `bar V`, with it's beginning point at the origin to simplify the idea that the x-component is the projection of the vector onto the x-axis. The angle, `phi`, between the x-axis and the vector, `bar V`, is used in this equation to compute the x-component of the vector, the projection of the vector, `bar V` onto the x-axis.
Figure B shows the Cartesian x and y components of the vector `bar V`. Figure B shows the vector `bar V` displaced from the vector shown in Figure A but the two vectors could be considered equivalent because they have the same length and they both point in the same direction.