Processing...

The Vector Calculator (3D) provides vector arithmetic functions for three dimensional vectors.

3D Vector Functions

k⋅V - scalar multiplication
V/k - scalar division
V / |V| - Computes the Unit Vector
|V| - Computes the magnitude of a vector
U + V - Vector addition
U - V - Vector subtraction
|U - V| - Distance between vector endpoints.
|U + V| - Magnitude of vector sum.
V • U - Computes the dot product of two vectors
V x U - Computes the cross product of two vectors
V x U • W - Computes the mixed product of three vectors
Vector Angle - Computes the angle between two vectors
Vector Area - Computes the area between two vectors
Vector Projection - Compute the vector projection of V onto U.
Vector Rotation - Compute the result vector after rotating around an axis.
Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
(ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
(x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
(r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
(x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
(x,y) to (r, θ) - Cartesian to Polar
(r, θ) to (x,y) - Polar to Cartesian
Vector Normal to a Plane Defined by Three Points

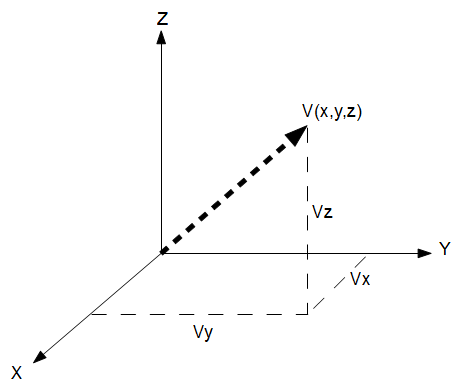
3 Dimensional Vectors

The Vector Calculator (3D) computes vector functions. Much of the mathematics applied to the world in which we live is through three dimensional vectors. The room in which you're sitting has an infinite number of points that can be located by their distance from any specific corner with three measurements: one from the floor, and two from perpendicular walls. In that case, the corner is the origin.

This is also true for coordinates on the Earth that are defined as distances from the center of the Earth with a z axis going from the center of the Earth through the North Pole, an x axis going from the center of the Earth through the Equator at longitude zero, and a y axis going from the center of the Earth through the Equator at longitude 90^o. This coordinates system is known as Earth Centered Fixed (ECF). Another coordinate system that is often used for satellites, is also centered in the Earth, except that the x coordinate is fixed to a point in space, the location of the vernal equinox. This is called Earth Centered Inertial (ECI). This is useful because the stars in the celestial sphere are relatively fixed in the ECI coordinate frame, and the slowly spinning Earth beneath the satellites can be ignored.

For these physical reasons and many more, 3D vector operations are important to understand and require precise computations in order to use them.

Dot Product (V • U)

In mathematics, the dot product, or scalar product (or sometimes inner product in the context of Euclidean space), is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. This operation can be defined either algebraically or geometrically. Algebraically, it is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. The name "dot product" is derived from the centered dot " · " that is often used to designate this operation; the alternative name "scalar product" emphasizes the scalar (rather than vectorial) nature of the result.

The formula for the dot product of two vectors (U and V) is:

d = (V_x * U_x+ V_y*U_y + V_z*U_v)

where:

d = vector dot product of V and U
V_x , V_y, V_z = components of vector V
U_x, U_y, U_z = components of vector U

Note: the arc-cosine (cosine inverse) of the dot product of two non-unit vectors does not produce the angle between the two vectors.

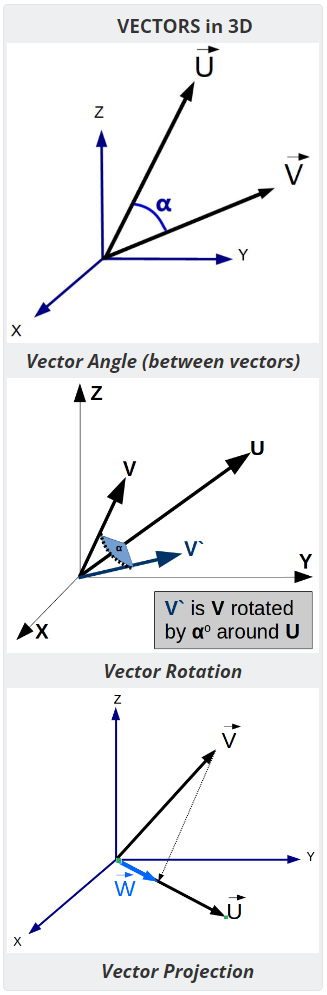
Angle Between Vectors

The angle between vectors formula lets the user enter two vectors (V and U) with X, Y and Z components (Euclidean 3-space vectors).

α = acos(`hatU * hatV`)

where:

α = angle between `vecV` and `vecU`
`hatU` = unit vector for `vecU`
`hatV` = unit vector for `vecV`

To calculate the angle between two vectors:

calculate the unit vectors associated with vector V and vector U. To do that,
1. compute the magnitude of the vectors and then
2. do a scalar multiplication for each of the vectors where the scalar(k) is the inverse of the vector's magnitude.
calculate the dot product of the unit vectors
calculate the arc-cosine of that dot product to calculate the angle between the vectors in radians.
converts radians to degrees.

Cross Product (V x U)

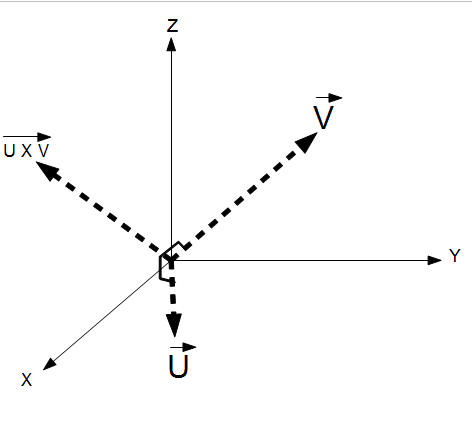mathematics, the cross product or vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ×. The cross product a × b of the vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, and engineering.

If the vectors have the same direction or one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, for perpendicular vectors, this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.

Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or "handedness". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.

Right Hand Convention: Note that cross product depicted in the diagram has the order of U X V, where U is first. This diagram shows the right and convention. Consider placing one's right hand along the first vector in the operation (U in the diagram). If one then sweeps the hand counter clockwise (normal right hand motion) 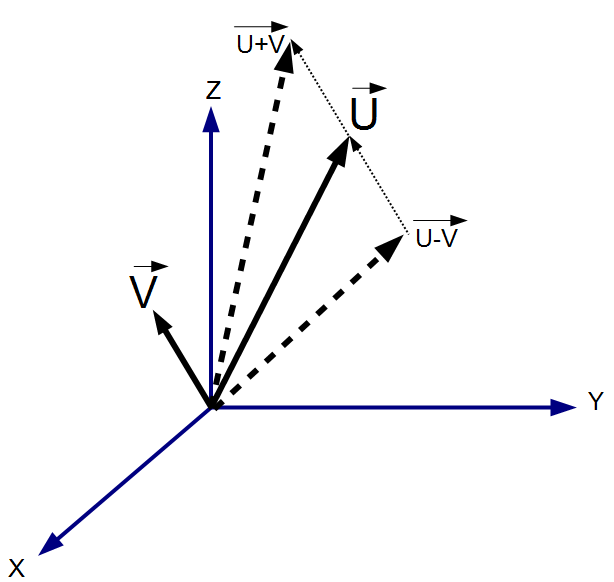towards the second vector (V in the diagram), the resulting normal vector (U X V) will be in the direction of one's extended thumb, hence the "Right Hand Convention".

Vector addition and subtraction (V +/- U)

The sum of two vectors (V, U) is the vector that results in the sum of the their respective components, such that U + V = (U_x+V_x, U_y+V_y, U_z+V_z). This can be seen visually (see diagram), by placing the origin of the second vector on the tip of the first. The resulting vector goes from the origin of the first vector and the tip of the second vector.

The difference of two vectors (V, U) is the vector that results in the difference of the their respective components, such that U - V = (U_x-V_x, U_y-V_y, U_z-V_z). This can be seen visually (see diagram), by placing the tip (as opposed to the origin) of the second vector on the tip of the first. The resulting vector goes from the origin of the first vector and the origin of the second vector.

Vector Rotation

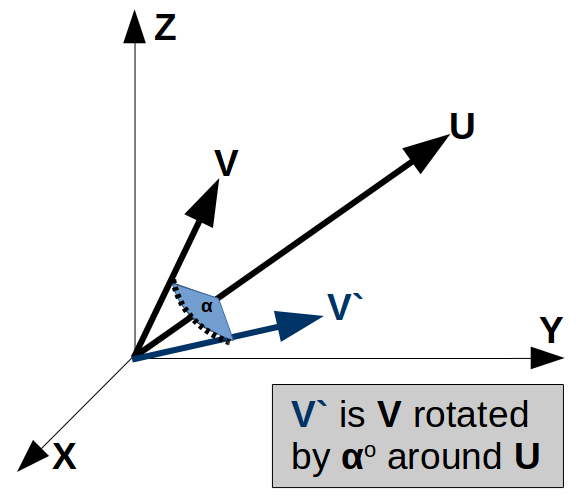A common function in 3D vectors is to perform a rotation about an axis. This is used in aerospace for things like attitude control in satellites and animation such as where an animated character's gun pointing (e.g. Woody in Toy Story). This Vector Rotation function uses quaternions to compute the result of the rotation of a vector (V) about an axis defined by another vector (U) for a prescribed angle (α). This rotation operates according to the "right hand rule". To understand this, think of the rotation vector (U) as the thumb on your right hand, and your index finger as the vector (V). The rotation angle is the counter-clockwise motion of your index finger during the rotation. Thanks to Damon Ostrander and Tom Sathre for their help with the quaternion math. CLICK HERE for Quaternion Calculator

The Vector Rotation formula uses quaternions to compute the resulting vector from the specified rotation. It uses the rotation of axis (U) and the rotation angle (α) to compute the quaternion of rotation (q). It then uses the quaternion vector rotation formula as follows:

V' = q⋅V⋅q^*
where:

V' is the rotated resultant vector.
q is the quaternion of rotation
q^* is conjugate of the quaternion of rotation.

Vector Projection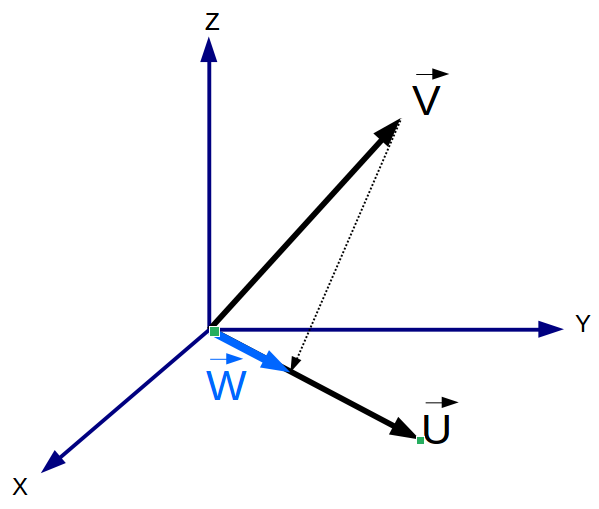

The vector projection of a vector V onto a nonzero vector U (also known as the vector component or vector resolution of V in the direction of U) is the orthogonal projection of V onto a straight line parallel to U.

To compute the projection of vector V onto vector U:

Compute the magnitude of vector V
Compute angle between vectors V and U
Compute the unit vector of vector U
Compute the scalar (k) associated with the projection which is the magnitude of V times the cosine of the angle between them.
Compute the vector resulting in the scalar multiplication of the unit vector of U and the scalar (k).

Spherical Coordinates

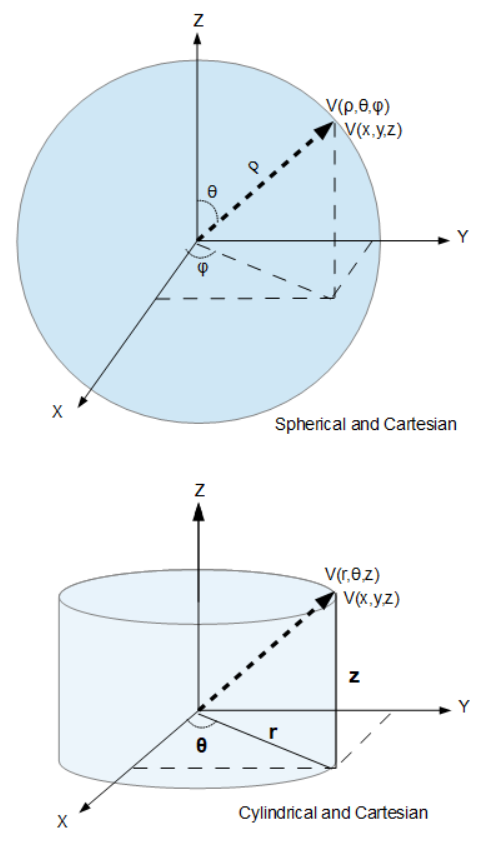In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane.

The radial distance is also called the radius or radial coordinate. The polar angle may be called co-latitude, zenith angle, normal angle, or inclination angle.

The use of symbols and the order of the coordinates differs between sources. In one system frequently encountered in physics (ρ, θ, φ) gives the radial distance, polar angle, and azimuthal angle, whereas in another system used in many mathematics books (ρ, θ, φ) gives the radial distance, azimuthal angle, and polar angle. In both systems ρ is often used instead of r. Other conventions are also used, so great care needs to be taken to check which one is being used.

A number of different spherical coordinate systems following other conventions are used outside mathematics. In a geographical coordinate system positions are measured in latitude, longitude and height or altitude. There are a number of different celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counter-clockwise rather than clockwise[further explanation needed]. The inclination angle is often replaced by the elevation angle measured from the reference plane. Elevation angle of zero is at the horizon.

The spherical coordinate system generalizes the two-dimensional polar coordinate system. It can also be extended to higher-dimensional spaces and is then referred to as a hyperspherical coordinate system.

Cylindrical Coordinates

In mathematics, a cylindrical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers:

(r) the radius of the base of the cylinder (r) with the center at the region that also intersects with the point,
(θ) the angle from the origin to the x,y plane (θ), and
(z) the elevation above or below the x,y plane (z)

University Contributors to vCalc

St Mary's College of Maryland

Reference

Wikipedia - en.wikipedia.org/wiki/Cross_product
Wikipedia - en.wikipedia.org/wiki/Dot_product
Wikipedia - en.wikipedia.org/wiki/Spherical_coordinate_system