La Calculadora de la macquina simple incluye las fórmulas para la calculación de las palancas, las correas, las poleas, y de los engranajes que contiene las ecuaciones relacionadas con las velocidades, los diámetros y las RPMs en sistemas de correas, de poleas y de engranajes. Las equaciones incluyen lo siguiente:

• La palanca (la longitud de la viga): Esta calculadora computa la longitud de una palanca (la viga) en el lado del fulcro necesario para levantar un objeto basarse en el peso del objeto y la longitud de la viga en el otro lado del fulcro. 
• La palanca (para levantar la masa):  Esta calculadora computa el peso que la palanca puede levantar basarse en la fuerza descendente y la longitud de la palanca en lo que sea lado del fulcro.
• La Posición del Fulcro (x): Esta calculadora computa la posición del fulcro necesario en una palanca para levantar un peso (W) con una fuerza descendente (F) con una viga de longitud (L), la ecuación: L = x + y.
• La Longitud de la Correa: Esta calculadora computa la longitud que está alrededor de los dos poleas basarse en los diámetros de las poleas y la distancia entre los ejes de la poleas. 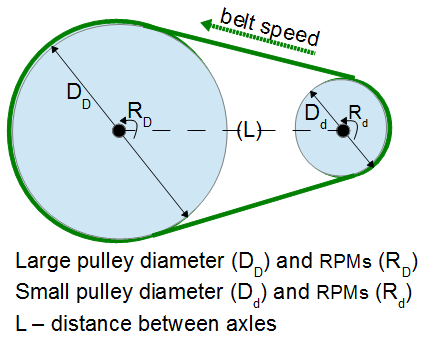  two pulley system
• La Velocidad de la Correa: Esta calculadora computa la velocidad que una longitud linear de la correa viaja alrededor de la polea basarse en el diámetro (D) de la polea y los revoluciónes (R) por minuto. 
• Polea Para Correa (RPM): Esta calculadora computa los revoluciónes por minuto de una polea basarse en la velocidad de la correa y el diámetro de la polea. 
• 2nd Pulley RPMs -  Esta calculadora computa los revoluciónes por minuto o RPMs del segundo polea basarse en los RPMs y el diámetro del primero polea y el diámetro del segundo polea.
• Segundo Polea (El Diámetro): Esta calculadora computa los revoluciónes por minuto del segundo polea cuando los revoluciónes por minuto y el diámetro del primero polea y el diámetro del segundo polea son conocido. 
• RPM del cuarto polea en tres astas: Esta calculadora computa los RPMs de la polea cuando los revoluciónes por minuto y los diámetros son conocido en tres ejes. 
• RPM del Segundo Engranaje: Esta calculadora computa los revoluciónes por minuto del segundo engranaje cuando los revoluciónes por minuto y el número de dientes del primero engranaje y el número de dientes del segundo engranaje son conocidos. 

Sistemas de correas y poleas

Un sistema de correa y polea se caracteriza por dos o más poleas en común a una correa. Esto permite que la potencia mecánica, el par de torsion, y la velocidad se transmitan a través de los ejes. Si las poleas son de diferente diámetros, se obtiene una ventaja mecánica. 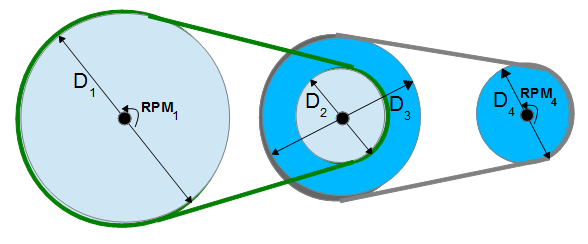 pulley transfer 

El empuje de una correa es simailar a el empuje de una cadena, pero una roldana para correa puede ser parejo (carente de miembros discretos de enclavamiento como se encontraría en un piñón de cadena, engranaje recto o correa dentada) de modo que la ventaja mecánica sea aproximadamente dada por la relación del diámetro de paso de las poleas solamente, no fijado exactamente por la relación de dientes como con engranajes y piñones. 

En el caso de una polea de tamor, sin ranura o bridas, la polea es a menudo ligeramente convexa para mantener centrada la cinta plana. A veces se la denomina polea coronada. Aunque una vez utilizado ampliamente en ejes de línea de fábrica, este tipo de polea todavía se encuentra conduciendo el cepillo giratorio en aspiradores verticales, en lijadores de cinta y sierras de cinta. Los tractores agrícolas construidos hasta principios de los años 1950 tenían generalmente una polea de correa para un cinturón plano (que es lo que la revista se nombró después). Ha sido sustituido por otros mecanismos con mayor flexibilidad en los métodos de uso, como las tomas de fuerza y las hidráulicas. 

Así como los diámetros de los engranajes (y en consecuencia, su número de dientes) determinan una relación de engranajes y, por lo tanto, los aumentos o reducciones de velocidad y la ventaja mecánica que pueden proporcionar, los diámetros de las poleas determinan esos mismos factores. Las poleas de cono y las poleas escalonadas (que funcionan tienden a aplicarse a versiones de banda plana y versiones de correa en V, respectivamente) son una forma de proporcionar múltiples relaciones de transmisión en un sistema de correa y polea que puede ser desplazado según sea necesario, del mismo modo que una transmisión proporciona a esta función un tren de engranajes que puede ser desplazado. Las poleas de paso de correa en V son la forma más común de que las perforadoras suministran una gama de velocidades de husillo. 

Las sistemas de los engranajes funcionan de manera similar como las poleas y las correas. , 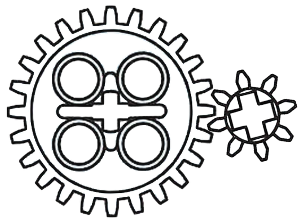         two gear system pero no hay una correa y los engranajes son entrelazan con los dientes de un engranaje para rotar los dientes del segundo engramaje.  En este caso, las revoluciónes por minuto o RPM es una función del número de dientes en el engramaje. La relación entre los engramajes: 

                                       `RPM_1 * Teeth_1 = RMP_2 *  Teeth_2`

Las Variables:

• RPM1 representa las revoluciónes por minuto del primero engranaje
• Teeth1 representa el número de dientes en el primero engramaje  
• RMP2 representa las revoluciónes por minuto del segundo engranaje 
• Teeth2 representa el número de dientes del segundo engranaje

The assumption is compatible teeth in the two gears.

Otras Calculadoras

• Pendulum -Esta calculadora usa las ecuaciónes para un péndulo.  
• Engine - Esta calculadora usa las ecuaciónes para motor de combustión. 

Referencias Bibliográficas

•  Wikipedia - http://en.wikipedia.org/wiki/Pulley

• Handyman In Your Pocket (2012 Richard A. Young and Thomas J. Glover) Sequoia Publishing of Littleton, CO.