La palanca (la longitud de la viga)

La calculadora para la longitud de una palanca usa la ecuación (y = x • W/F ) para calcular la longitud 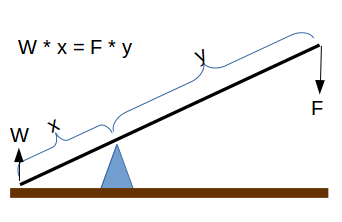  Lever with beam (x+y) and fulcrum.(y) en el lado de la fuerza del fulcro del punto de apoyo para levantar un objeto con una palanca. 

INSTRUCCIONES: Elija sus unidades preferidas e ingrese lo siguiente:

• (F)  La fuerza hacia abajo (el peso) opuesta al fulcro desde el objeto. 
• (W) El peso del objeto que es levantado por la palanca. 
• (x) La longitud de la viga en el lado del objeto del fulcro (ver diagrama)  

La calculadora computa la longitud de la viga (y) en metros. Sin embargo, esto se puede convertir automáticamente a otras unidades de longitud a través del menú desplegable.

Utilización

Si montas una palanca (el haz y el fulcro), esta fórmula le indicará la longitud necesaria para levantar la masa. Suponga que poner todo su peso en el extremo de la viga, 200 libras, y que desea levantar 1,400 libras. Esta fórmula le dira2 que si hay 6 pulgadas de la viga en el lado masivo del fulcro, el peso debe estar en la marca de 3.5 pies (42 pulgadas) en el otro lado para levantar el objeto. 

Calculadoras relacionadas

• Para computar el peso (W) que se puede levantar con una palanca basada en la longitud de la viga (y) sobre el fulcro, la longitud (x) debajo del fulcro y el peso hacia abajo aplicado  (F), Haz click aquí. 
• Para computar la longitud (x) del objeto a el fulcro necesario en una palanca para levantar un peso (W) con una fuerza descendente (F) con una viga de longitud (L), la ecuación: L = x + y, Haz click aquí. 

La Maquina Simple (La Fisica)

• La palanca (la longitud de la viga): Esta calculadora computa la longitud de una palanca (la viga) en el lado del fulcro necesario para levantar un objeto basarse en el peso del objeto y la longitud de la viga en el otro lado del fulcro. 
• La palanca (para levantar la masa):  Esta calculadora computa el peso que la palanca puede levantar basarse en la fuerza descendente y la longitud de la palanca en lo que sea lado del fulcro.
• La Posición del Fulcro (x): Esta calculadora computa la posición del fulcro necesario en una palanca para levantar un peso (W) con una fuerza descendente (F) con una viga de longitud (L), la ecuación: L = x + y.
• La Longitud de la Correa: Esta calculadora computa la longitud que está alrededor de los dos poleas basarse en los diámetros de las poleas y la distancia entre los ejes de la poleas.
• La Velocidad de la Correa: Esta calculadora computa la velocidad que una longitud linear de la correa viaja alrededor de la polea basarse en el diámetro (D) de la polea y los revoluciónes (R) por minuto. 
• Polea Para Correa (RPM): Esta calculadora computa los revoluciónes por minuto de una polea basarse en la velocidad de la correa y el diámetro de la polea. 
• 2nd Pulley RPMs -  Esta calculadora computa los revoluciónes por minuto o RPMs del segundo polea basarse en los RPMs y el diámetro del primero polea y el diámetro del segundo polea.
• Segundo Polea (El Diámetro): Esta calculadora computa los revoluciónes por minuto del segundo polea cuando los revoluciónes por minuto y el diámetro del primero polea y el diámetro del segundo polea son conocido. 
• RPM del cuarto polea en tres astas: Esta calculadora computa los RPMs de la polea cuando los revoluciónes por minuto y los diámetros son conocido en tres ejes. 
• RPM del Segundo Engranaje: Esta calculadora computa los revoluciónes por minuto del segundo engranaje cuando los revoluciónes por minuto y el número de dientes del primero engranaje y el número de dientes del segundo engranaje son conocidos.