La Ecuacion de Van't Hoff

La Ecuación de Van't Hoff, ln(K₂/K₁) = ΔH⁰/R (1/T₁ - 1/T₂), proporciona información sobre la dependencia de la temperatura de la el constante de equilibrio. Esta ecuación fue propuesta en el año 1884 por Jacobus Henricus van't Hoff. Van't Hoff hizo grandes contribuciónes a la química física, específicamente en la cinética química, la estereoquímica, y el equilibrio químico.

INSTRUCCIONES: Elija sus unidades preferidas e ingrese lo siguiente:

• K₁ representa el constante de equilibrio en temperatura absoluta T₁.
• K₂ representa el constante de equilibrio en temperatura absoluta T₂.
• T₁ es la temperatura absoluta.
• T₂ es la segunda temperatura absoluta.

ΔH⁰: La calculadora devuelve la entalpía de reacción (el calor estándar de la reacción). Esta calculadora utiliza el constante de gas, Constante de Gas Ideal (R):8.3144626181532 J/(mol·K).

Todas las temperaturas se convierten automáticamente a Kelvin.

La Matemáticas

La fórmula en esta ecuación es la siguiente:

          `ΔH^0 = R * ( -ln(K_2/K_1))/ (1/T_1 - 1/T_2)` 

Es una forma de: ln(K₂/K₁) = ΔH⁰/R (1/T₁ - 1/T₂) solved for  ΔH⁰.

Descripción

Si se conocen los constantes de equilibrio para dos temperaturas diferentes, entonces se puede encontrar ΔH⁰ de una sustancia.  Asimismo, si  se conoce un constante de equilibrio (K₁) para T₁ y ΔH⁰, entonces se puede calcular la constante de equilibrio (K₂) para una segunda temperatura. La ecuación de Van't Hoff supone que ΔH⁰ no cambia con la temperatura. Esto no es necesariamente cierto; ΔH⁰ cambia con la temperatura, pero el cambio es lo suficientemente pequeño como para que se considere insignificante al estimar K₂. 

Cuando el constante de equilibrio y la temperatura se trazan entre sí, tanto una reacción exotérmica como una reacción endotérmica tendrán una forma característica en su gráfica. Los gráficos exotérmicos tienden a ser lineales con una pendiente positiva, mientras que las reacciones endotérmica son lineales con una pendiente negativa, como se muestra a continuación. 

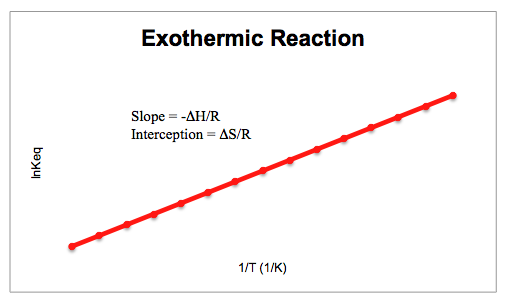
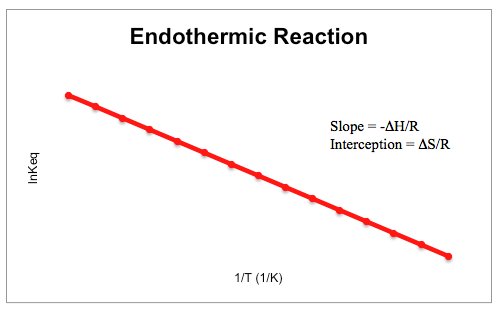
Temas relacionados

Ecuación de Arrhenius (para encontrar k) 

Clausius-Clapeyron Equation

Referencias Bibliográficas

Whitten, et al. "Chemistry" 10th Edition. Pp. 699

Wikipedia: Van't Hoff Equation
)))