Sallen-Key Unity Gain Low Pass Filter - Transfer Function
Tags | |
UUID | 81b3a72c-3d38-11e3-83ad-bc764e049c3d |
The Sallen-Key Unity Gain Low Pass Filter - Transfer Function calculator computes the transfer function H(s) for a unity gain low pass filter implementation of the Sallen-Key topology.
INSTRUCTIONS: Choose units and the following:
- (α) Attenuation factor
- (s) Complex angular frequency
- (ω0) Undampended Angular Frequency
Transfer Function H(s): The calculator return the transfer function value as a unit-less real number.
The Math / Science
The Sallen- Key filter is an active filter used to create 2nd order filter stages that can be cascaded together to form larger order filters. The op-amp provides buffering between filter stages, so that each stage can be designed independently of the others. These circuits are suitable for filters which have complex conjugate poles. When implementing a particular transfer function, a designer will typically find all of the poles, and group them into real poles and complex conjugate pairs. Each of the complex conjugate pole pares are then implemented with a Sallen-Key filter, and the circuits are cascaded together to form the complete filter.
TRANSFER FUNCTION: A transfer function, H(s), of an electronic or control system component is a mathematical function describing the output value for each possible input value to the device. It is often represented as a transfer curve or characteristic curve.
The transfer function characterizes the behavior of a component in a system. The transfer function can be used in the analysis of systems such as: electronics control systems, project management systems, and construction management systems.
ATTENUATION: the reduction of the amplitude of a signal, electric current, or other oscillation.
This electronic filter is a special case of a second-order unity gain filter version of the voltage-controlled voltage-source (VCVS) topology. We derive the equation as follows using s for seconds:
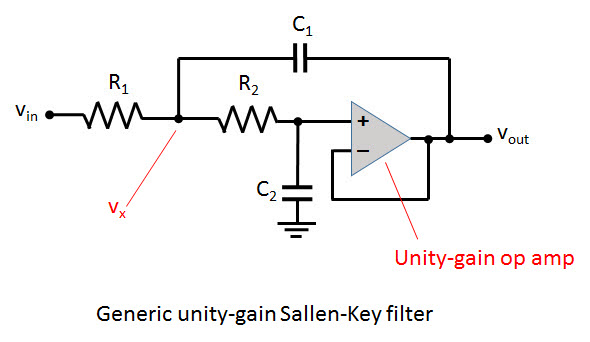
eq 1: Vx=iC2⋅R2+Vout
eq 2: Vx=Vout⋅R2⋅C2⋅s+Vout
eq 3: Vx=Vout(R2⋅C2⋅s+1)
Next look at the sum of currents at V1:
eq 4: iC2=iC1+iR1
eq 5: Vout1s⋅C2=Vin-VxR1+Vout-Vx1s⋅C1
eq 6 : s⋅R1⋅C2⋅Vout=Vin-Vx+s⋅R1⋅C1⋅(Vout-Vx)
Substituting for Vx using eq 3 and rearranging eq 6:
eq 7: s⋅R1⋅C2⋅Vout=Vin-Vout(R2⋅C2⋅s+1)+s⋅R1⋅C1⋅Vout-s⋅R1⋅C1(R2⋅C2⋅s+1)⋅Vout
Rearranging so all terms with a factor of Vout are on the left:
eq 8: Vout⋅[(s⋅R1⋅C2)+(s⋅R2⋅C2+1)+(s⋅R1⋅C1(s⋅R2⋅C2+1))-(s⋅R1⋅C1)]=Vin
Now rearranging eq 8:
eq 9: Vout[(s2⋅R1⋅R2⋅C1⋅C2)+s(R1⋅C2+R2⋅C2)+1]=Vin
Defining VoutVin to be out transfer function H(s)
eq 10: H(s)[(s2⋅R1⋅R2⋅C1⋅C2)+s(R1⋅C2+R2⋅C2)+1]=1
Divide both sides by R1⋅R2⋅C1⋅C2
eq 11: H(S)[s2+s(R1⋅C2R1⋅R2⋅C1⋅C2+R2⋅C2R1⋅R2⋅C1⋅C2)+(1R1⋅R2⋅C1⋅C2)]=1R1⋅R2⋅C1⋅C2
Factoring the terms
eq 12: H(S)[s2+s(R1⋅C2R2⋅C1+1R1⋅C1)+(1R1⋅R2⋅C1⋅C2)]=1R1⋅R2⋅C1⋅C2
Dividing both sides by the term in square brackets
eq 12: H(S) =1R1⋅R2⋅C1⋅C2s2+s(R1⋅C2R2⋅C1+1R1⋅C1)+(1R1⋅R2⋅C1⋅C2)
We then define ω20=1R1⋅R2⋅C1⋅C2
eq 13: H(S) =ω20s2 +s(R1⋅C2R2⋅C1+1R1⋅C1)+ ω20
And 2α=R1⋅C2R2⋅C1+1R1⋅C1
Sallen-Key Calculators:
- Comments
- Attachments
- Stats
No comments |

