The Sallen-Key Unity Gain Low Pass Filter - Transfer Function calculator computes the transfer function H(s) for a unity gain low pass filter implementation of the Sallen-Key topology.
INSTRUCTIONS: Choose units and the following:
- (α) Attenuation factor
- (s) Complex angular frequency
- (ω0) Undampended Angular Frequency
Transfer Function H(s): The calculator return the transfer function value as a unit-less real number.
The Math / Science
The Sallen- Key filter is an active filter used to create 2nd order filter stages that can be cascaded together to form larger order filters. The op-amp provides buffering between filter stages, so that each stage can be designed independently of the others. These circuits are suitable for filters which have complex conjugate poles. When implementing a particular transfer function, a designer will typically find all of the poles, and group them into real poles and complex conjugate pairs. Each of the complex conjugate pole pares are then implemented with a Sallen-Key filter, and the circuits are cascaded together to form the complete filter.
TRANSFER FUNCTION: A transfer function, H(s), of an electronic or control system component is a mathematical function describing the output value for each possible input value to the device. It is often represented as a transfer curve or characteristic curve.
The transfer function characterizes the behavior of a component in a system. The transfer function can be used in the analysis of systems such as: electronics control systems, project management systems, and construction management systems.
ATTENUATION: the reduction of the amplitude of a signal, electric current, or other oscillation.
This electronic filter is a special case of a second-order unity gain filter version of the voltage-controlled voltage-source (VCVS) topology. We derive the equation as follows using s for seconds:
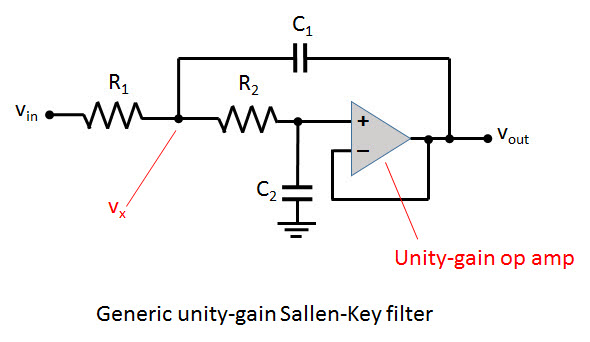
eq 1: `V_x = i_"C2" * R_2 + V_"out"`
eq 2: `V_x = V_"out" * R_2 * C_2 *s + V_"out"`
eq 3: `V_x = V_"out" (R_2 * C_2 *s +1)`
Next look at the sum of currents at `V_1`:
eq 4: `i_"C2" = i_"C1" + i_"R1"`
eq 5: `V_"out"/(1/(s*C_2)) = (V_"in" - V_x)/R_1 + (V_"out" -V_x) / (1/(s*C_1))`
eq 6 : `s*R_1*C_2* V_"out" = V_"in" - V_x + s*R_1*C_1* (V_"out" - V_x)`
Substituting for `V_x` using eq 3 and rearranging eq 6:
eq 7: `s* R_1 *C_2* V_"out" = V_"in" - V_"out"(R_2* C_2*s +1) + s*R_1*C_1*V_"out" - s*R_1*C_1 (R_2*C_2 *s +1) *V_"out"`
Rearranging so all terms with a factor of `V_"out"` are on the left:
eq 8: `V_"out" * [(s*R_1*C_2) + (s* R_2*C_2 +1) + (s*R_1*C_1 (s*R_2*C_2 +1)) - (s*R_1*C_1)] = V_"in"`
Now rearranging eq 8:
eq 9: `V_"out" [ (s^2 *R_1*R_2*C_1*C_2) +s (R_1*C_2 +R_2*C_2) + 1 ] = V_"in"`
Defining `V_"out"/V_"in"` to be out transfer function H(s)
eq 10: `H(s) [ (s^2 *R_1*R_2*C_1*C_2) +s (R_1*C_2 +R_2*C_2) + 1 ] = 1`
Divide both sides by `R_1*R_2*C_1*C_2`
eq 11: `H(S) [s^2 +s ((R_1*C_2)/(R_1*R_2*C_1*C_2) +(R_2*C_2)/(R_1*R_2*C_1*C_2)) +(1/(R_1*R_2*C_1*C_2)) ] = 1/(R_1*R_2*C_1*C_2)`
Factoring the terms
eq 12: `H(S) [s^2 +s ((R_1*C_2)/(R_2*C_1) + 1/(R_1*C_1)) +(1/(R_1*R_2*C_1*C_2)) ] = 1/(R_1*R_2*C_1*C_2)`
Dividing both sides by the term in square brackets
eq 12: `H(S) = (1/(R_1*R_2*C_1*C_2))/(s^2 +s ((R_1*C_2)/(R_2*C_1) + 1/(R_1*C_1)) +(1/(R_1*R_2*C_1*C_2))`
We then define `omega_0^2 = 1/(R_1*R_2*C_1*C_2)`
eq 13: `H(S) = omega_0^2/(s^2 + s ((R_1*C_2)/(R_2*C_1) + 1/(R_1*C_1)) + omega_0^2)`
And `2 alpha = (R_1*C_2)/(R_2*C_1) + 1/(R_1*C_1)`
