Slant Range (Vector)

The Slant Range using Vectors calculator computes the slant range (R) from a ground station to an object (satellite or aircraft) based on the station and object position vectors.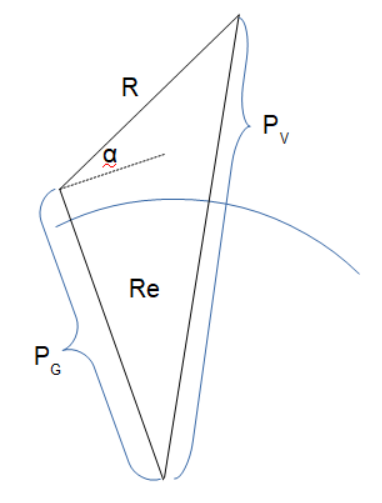

INSTRUCTIONS: Enter the following:

• (P_G) Ground Station Position Vector (kilometer units) 
• (P_V) Vehicle Position Vector (kilometers units) 

Slant Range (R):  The range is returned in kilometers.  However this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The formula for the slant range uses both the law of sines and the law of cosines.   In the obtuse triangle below: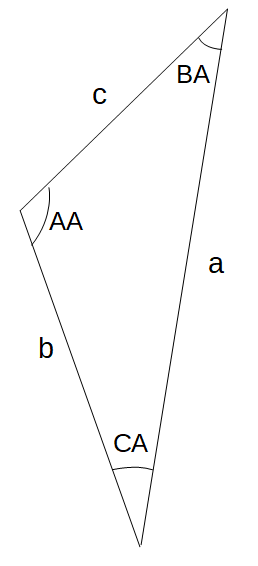

• b = Re + sA
• a = Re + oA
• c is the slant range
• CA is the Earth Central Angle
• BA is the subtended angle (β)
• AA is elevation angle (α) + 90°

Law of Sines:

      `a/(sin("AA")) = b / (sin("BA")) = c / (sin("CA"))`

Law of Cosines:

       `c = sqrt( a^2 + b^2 - 2a*b*cos(CA) )`

Earth Model Calculators

• Slant Range using Position Vectors
• Slant Range from Elevation Angle (α)
• Slant Range using Subtended Angle (β)
• Distance to Horizon
• Angle of Satellite Visibility
• Grazing Angle
• XYZ to Latitude, Longitude, Altitude
• Earth WGS-84 Equatorial radius in meters: 6378137.0 m
• Earth WGS-84 Polar radius in meters: 6356752.31424518 m 
• Earth Flattening Factor (WGS-84): 0.00335281066474748071984552861852
• Ellipse flattening factor: F = (Er - Pr)/Er  
• Geocentric to Geodetic Latitude
• Geodetic to Geocentric Latitude

3D Vector Functions

• k⋅V - scalar multiplication
• V/k - scalar division
• V / |V| - Computes the Unit Vector
• |V| - Computes the magnitude of a vector
• U + V - Vector addition
• U - V - Vector subtraction
• |U - V| - Distance between vector endpoints.
• |U + V| - Magnitude of vector sum.
• V • U - Computes the dot product of two vectors
• V x U - Computes the cross product of two vectors
• V x U • W - Computes the mixed product of three vectors
• Vector Angle - Computes the angle between two vectors
• Vector Area - Computes the area between two vectors
• Vector Projection - Compute the vector projection of V onto U.
• Vector Rotation - Compute the result vector after rotating around an axis.
• Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
• (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
• (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
• (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
• (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
• (x,y) to (r, θ) - Cartesian to Polar
• (r, θ) to (x,y) - Polar to Cartesian 
• Vector Normal to a Plane Defined by Three Points