The Unit Vector Normal to a Plane calculator computes the normal unit vector to a plane defined by three points in a three dimensional cartesian coordinate frame.
INSTRUCTIONS: Enter the following:
- (P1) Point 1 (e.g. 2,3,4)
- (P2) Point 2 (e.g. 5,6,7)
- (P3) Point 3 (e.g. 1,8,9)
Normal Unit Vector to the Plane (V): The calculator returns the vector normal to the plane defined by the three points.
NOTE: Positions in 3D and vectors are entered via comma separate strings (e.g. 4,12,-2).
The Math / Science
To compute the normal vector to a plane created by three points:
- Create three vectors (A,B,C) from the origin to the three points (P1, P2, P3) respectively.
- Using vector subtraction, compute the vectors U = A - B and W = A - C
- Compute the vector cross product, V = U x W
- Compute the unit vector of V, `hatV = vecV/(|vecV|)`
`hatV` is the unit vector normal to the plane created by the three points.
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
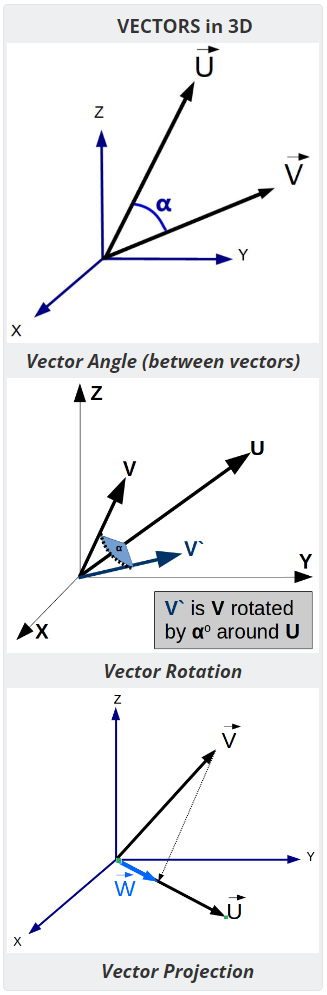
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points

