Tags | |
The Baguette Cut Diamond Weight calculator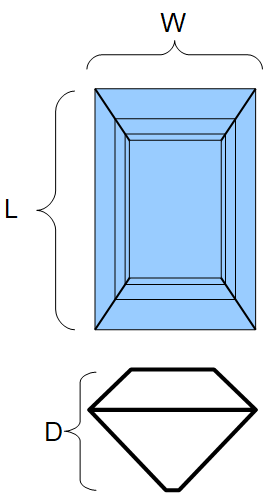
computes the approximate carat weight of a baguette cut diamond based on the vertical and horizontal widths, and the depth.
INSTRUCTIONS: Choose units and enter the following:
- (L) Length
- (W) Width
- (D) Depth
Baguette Cut Diamond Carat Weight (w): The calculator returns weight of the diamond in carats. However, this can be automatically converted to other weight units (e.g. grams) via the pull-down menu.
Diamond Carat Weight Calculator
This jewelers suite of calculators includes carat weight estimations of diamonds based on the cut diamonds shape and size that can be measured while still within a setting. This enables the jeweler to estimate the carat weigh of the diamond without damaging the setting. 
The diamond weight formulas contain carat weight equations that are specific to diamonds and diamond cuts:
- Compute carat weight of Round Brilliant diamond
- Compute carat weight of Oval Brilliant diamond
- Compute carat weight of Heart Shaped diamond
- Compute carat weight of Emerald Cut diamond
- Compute carat weight of Baguette diamond
- Compute carat weight of Princess Cut diamond
- Compute carat weight of Triangular Brilliant diamond
- Compute carat weight of Marquise Brilliant diamond
- Compute carat weight of Pear Shaped Brilliant (Teardrop) diamond
- Compute carat weight of Tapered Baguette diamond
- Compute carat weight of Old European cut diamond
- Compute carat weight of Cushion diamond
ACCURACY COMPARISON
The carat weight equations and data used in vCalc's jewelry library and calculator were reviewed by a certified gemologist. The equations are based on industry recognized formulas and data. The table below shows a comparison of computations between vCalc and an industry accepted application (Quantum Leap).
The length, width and depth are in millimeters (mm), and the Quantum Leap and vCalc measurements are in carats (cwt).
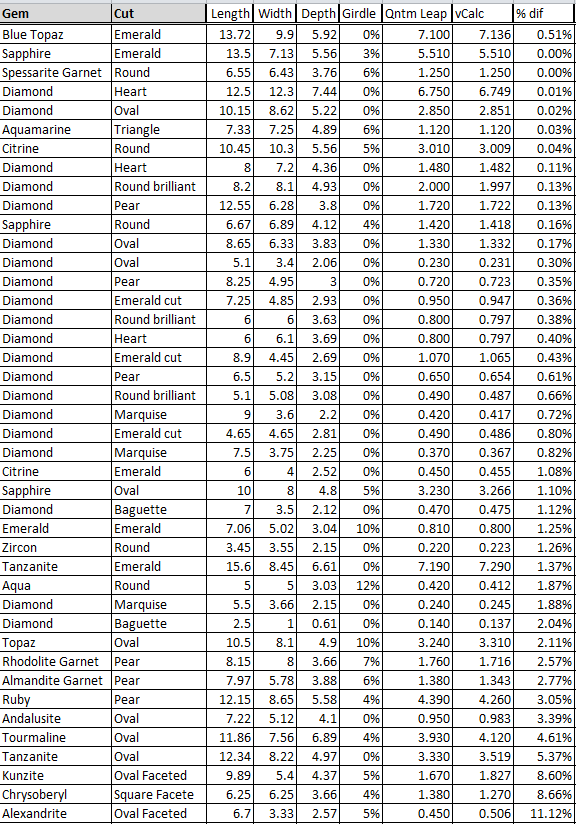
The largest variance, an oval faceted alexandrite, which can be seen in the last row above, has been double checked against several source equations which tend to support vCalc's accuracy.
