The Bell-shaped Height calculator computes the height associated with a bell-shaped object.
INSTRUCTIONS: Choose units and enter the following:
- (W) Width of Bell-shape
Bell-shaped Height (H): The calculator returns the height in meters. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
A bell-shaped area can be create by the intersection of two equal but reversed circle sectors (pieces of a pie) where the angle of the circle sector is 60°. This creates an interior equilateral triangle (see diagram).
The formula for the height of a bell-shaped object is:
h = tan(π/3) ⋅ (W/2)
where:
- h = height of bell-shaped object
- W = base width of bell-shaped object
- π/3 = 60°
Bell-shaped Objects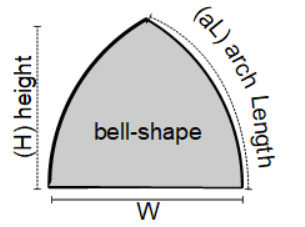
- Area of Bell-shaped Object
- Height of Bell-shaped Object
- Arc Length of Bell-shaped Object
- Volume of Bell-shaped Greenhouse
A bell-shaped area can be create by the intersection of two equal but reversed circle sectors (pieces of a pie) where the angle of the circle sector is 60° (π/3 radians). This creates an interior equilateral triangle (see diagram).
