Osmotic Pressure
From UCDavis Chemwiki
Osmotic pressure is a colligative property of solutions that is observed using a semipermeable membrane, a barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions. The net flow of solvent through a semipermeable membrane is called osmosis (from the Greek osmós, meaning “push”). The direction of net solvent flow is always from the side with the lower concentration of solute to the side with the higher concentration.
Osmosis can be demonstrated using a U-tube like the one shown in Figure 14.4.2 "Osmotic Pressure", which contains pure water in the left arm and a dilute aqueous solution of glucose in the right arm. A net flow of water through the membrane occurs until the levels in the arms eventually stop changing, which indicates that equilibrium has been reached. The osmotic pressure (Π) of the glucose solution is the difference in the pressure between the two sides, in this case the heights of the two columns. Although the semipermeable membrane allows water molecules to flow through in either direction, the rate of flow is not the same in both directions because the concentration of water is not the same in the two arms. The net flow of water through the membrane can be prevented by applying a pressure to the right arm that is equal to the osmotic pressure of the glucose solution.
Figure 16 Osmotic Pressure
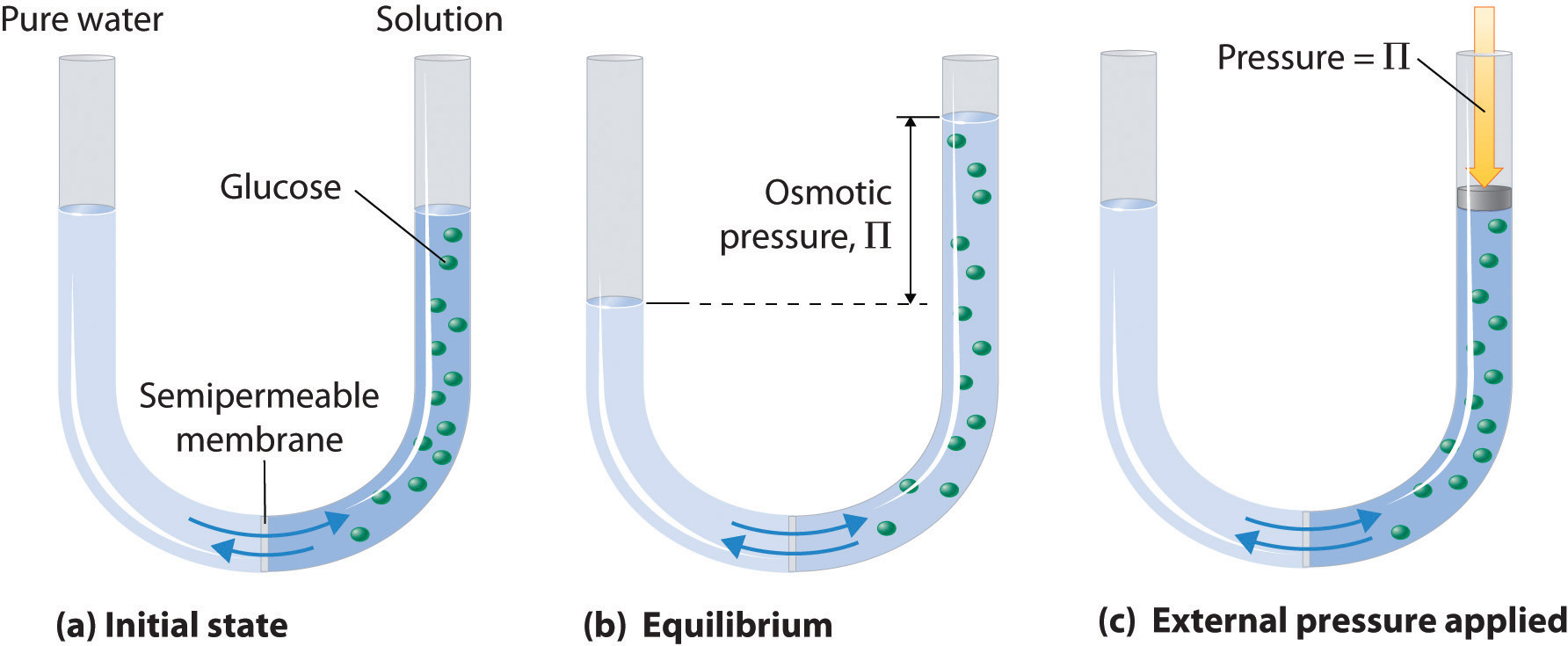
(a) A dilute solution of glucose in water is placed in the right arm of a U-tube, and the left arm is filled to the same height with pure water; a semipermeable membrane separates the two arms. Because the flow of pure solvent through the membrane from left to right (from pure water to the solution) is greater than the flow of solvent in the reverse direction, the level of liquid in the right tube rises. (b) At equilibrium, the pressure differential, equal to the osmotic pressure of the solution (Πsoln), equalizes the flow rate of solvent in both directions. (c) Applying an external pressure equal to the osmotic pressure of the original glucose solution to the liquid in the right arm reverses the flow of solvent and restores the original situation.
Just as with any other colligative property, the osmotic pressure of a solution depends on the concentration of dissolved solute particles. Osmotic pressure obeys a law that resembles the ideal gas equation:
Osmotic Pressure (Π):
where M is the number of moles of solute per unit volume of solution (n/V i.e., the molarity of the solution), R is the ideal gas constant (0.0821 L*atm/mol*K), and T is the absolute temperature. As shown in the following example, osmotic pressures tend to be quite high, even for rather dilute solutions.
Example 11 When placed in a concentrated salt solution, certain yeasts are able to produce high internal concentrations of glycerol to counteract the osmotic pressure of the surrounding medium. Suppose that the yeast cells are placed in an aqueous solution containing 4.0% NaCl by mass; the solution density is 1.02 g/mL at 25°C.
Calculate the osmotic pressure of a 4.0% aqueous NaCl solution at 25°C.
If the normal osmotic pressure inside a yeast cell is 7.3 atm, corresponding to a total concentration of dissolved particles of 0.30 M, what concentration of glycerol must the cells synthesize to exactly balance the external osmotic pressure at 25°C?
Solution:
The solution contains 4.0 g of NaClNaCl per 100 g of solution. Using the formula mass of NaClNaCl (58.44 g/mol) and the density of the solution (1.02 g/mL), we can calculate the molarity:
`M_(NaCl)=("moles NaCl")/("liter solution")`
`=((4.0 cancel(g)" "NaCl )/(58.44 cancel(g)"/"mol " " NaCl)) ((1)/(100 cancel(g " solution"))) ((1.02 cancel(g " solution")/(1.00 cancel(mL) " solution")) ((1000mL)/(1L))`
`=0.70 M " " NaCl`
Because 1 mol of NaCl produces 2 mol of particles in solution, the total concentration of dissolved particles in the solution is (2)(0.70 M) = 1.4 M.
B Now we can use osmotic pressure equation to calculate the osmotic pressure of the solution:
`Π = MRT`
`=(1.4mol"/"L)[0.0821 (L*atm)"/"(K*mol)](298K)`
`=34 atm`
C If the yeast cells are to exactly balance the external osmotic pressure, they must produce enough glycerol to give an additional internal pressure of (34 atm − 7.3 atm) = 27 atm. Glycerol is a nonelectrolyte, so we can solve the osmotic pressure equation for the molarity corresponding to this osmotic pressure:
`M=(Π)/(RT)`
`=(27 cancel(atm))/([0.0821(L*cancel(atm))"/"(cancel(K)*mol)](298cancel(K))`
`=1.1 M" " glycerol`
In solving this problem, we could also have recognized that the only way the osmotic pressures can be the same inside the cells and in the solution is if the concentrations of dissolved particles are the same. We are given that the normal concentration of dissolved particles in the cells is 0.3 M, and we have calculated that the NaClNaCl solution is effectively 1.4 M in dissolved particles. The yeast cells must therefore synthesize enough glycerol to increase the internal concentration of dissolved particles from 0.3 M to 1.4 M—that is, an additional 1.1 M concentration of glycerol.