11.2 Energy by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

11.2 Energy

The analysis based on friction is somewhat superficial, however. One could understand friction perfectly well and yet imagine the following situation. Astronauts bring back a piece of magnetic ore from the moon which does not behave like ordinary magnets. A normal bar magnet, c/1, attracts a piece of iron essentially directly toward it, and has no left- or right-handedness. The moon rock, however, exerts forces that form a whirlpool pattern around it, 2. NASA goes to a machine shop and has the moon rock put in a lathe and machined down to a smooth cylinder, 3. If we now release a ball bearing on the surface of the cylinder, the magnetic force whips it around and around at ever higher speeds. Of course there is some friction, but there is a net gain in speed with each revolution.

Physicists would lay long odds against the discovery of such a moon rock, not just because it 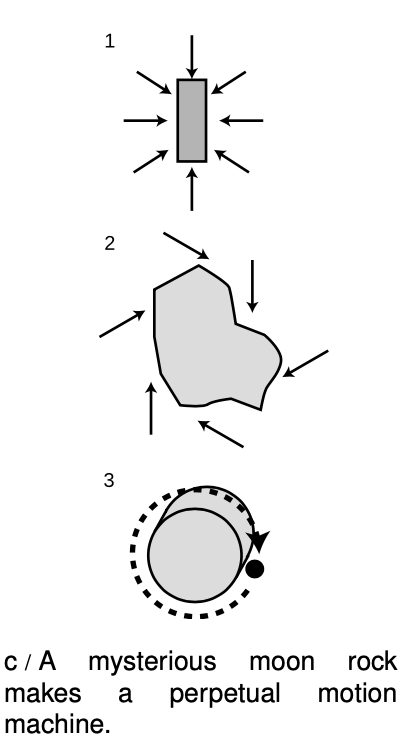breaks the rules that magnets normally obey but because, like the alchemists, they have discovered a very deep and fundamental principle of nature which forbids certain things from happening. The first alchemist who deserved to be called a chemist was the one who realized one day, “In all these attempts to create gold where there was none before, all I've been doing is shuffling the same atoms back and forth among different test tubes. The only way to increase the amount of gold in my laboratory is to bring some in through the door.” It was like having some of your money in a checking account and some in a savings account. Transferring money from one account into the other doesn't change the total amount.

We say that the number of grams of gold is a conserved quantity. In this context, the word “conserve” does not have its usual meaning of trying not to waste something. In physics, a conserved quantity is something that you wouldn't be able to get rid of even if you wanted to. Conservation laws in physics always refer to a closed system, meaning a region of space with boundaries through which the quantity in question is not passing. In our example, the alchemist's laboratory is a closed system because no gold is coming in or out through the doors.

Example 1: Conservation of mass

In figure d, the stream of water is fatter near the mouth of the faucet, and skinnier lower down. This is because the water speeds up as it falls. If the cross-sectional area of the stream was equal all along its length, then the rate of flow through a lower cross-section would be greater than the rate of flow through a cross-section higher up. Since the flow is steady, the amount of water between the two cross-sections stays constant. The cross-sectional area of the stream must therefore shrink in inverse proportion to the increasing speed of the falling water. This is an example of conservation of mass.

In general, the amount of any particular substance is not conserved. Chemical reactions can change one substance into another, and nuclear reactions can even change one element into another. The total mass of all substances is however conserved:

A similar lightbulb eventually lit up in the heads of the people who had been frustrated trying to build a perpetual motion machine. In perpetual motion machine a, consider the motion of one of the balls. It performs a cycle of rising and falling. On the way down it gains speed, and coming up it slows back down. Having a greater speed is like having more money in your checking account, and being high up is like having more in your savings account. The device is simply shuffling funds back and forth between the two. Having more balls doesn't change anything fundamentally. Not only that, but friction is always draining off money into a third “bank account:” heat. The reason we rub our hands together when we're cold is that kinetic friction heats things up. The continual buildup in the “heat account” leaves less and less for the “motion account” and “height account,” causing the machine eventually to run down.

These insights can be distilled into the following basic principle of physics:

The moon rock story violates conservation of energy because the rock-cylinder and the ball together constitute a closed system. Once the ball has made one revolution around the cylinder, its position relative to the cylinder is exactly the same as before, so the numerical energy rating associated with its position is the same as before. Since the total amount of energy must remain constant, it is impossible for the ball to have a greater speed after one revolution. If it had picked up speed, it would have more energy associated with motion, the same amount of energy associated with position, and a little more energy associated with heating through friction. There cannot be a net increase in energy.

Example 2: Converting one form of energy to another

Dropping a rock: The rock loses energy because of its changing position with respect to the earth. Nearly all that energy is transformed into energy of motion, except for a small amount lost to heat created by air friction.

Sliding in to home base: The runner's energy of motion is nearly all converted into heat via friction with the ground.

Accelerating a car: The gasoline has energy stored in it, which is released as heat by burning it inside the engine. Perhaps 10% of this heat energy is converted into the car's energy of motion. The rest remains in the form of heat, which is carried away by the exhaust.

Cruising in a car: As you cruise at constant speed in your car, all the energy of the burning gas is being converted into heat. The tires and engine get hot, and heat is also dissipated into the air through the radiator and the exhaust.

Stepping on the brakes: All the energy of the car's motion is converted into heat in the brake shoes.

Example 3: Stevin's machine

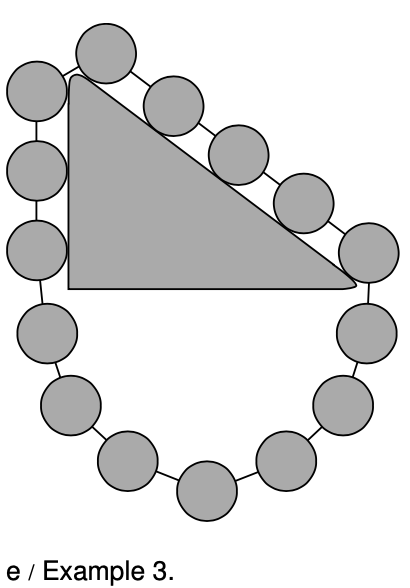The Dutch mathematician and engineer Simon Stevin proposed the imaginary machine shown in figure e, which he had inscribed on his tombstone. This is an interesting example, because it shows a link between the force concept used earlier in this course, and the energy concept being developed now.

The point of the imaginary machine is to show the mechanical advantage of an inclined plane. In this example, the triangle has the proportions 3-4-5, but the argument works for any right triangle. We imagine that the chain of balls slides without friction, so that no energy is ever converted into heat. If we were to slide the chain clockwise by one step, then each ball would take the place of the one in front of it, and the over all configuration would be exactly the same. Since energy is something that only depends on the state of the system, the energy would have to be the same. Similarly for a counterclockwise rotation, no energy of position would be released by gravity. This means that if we place the chain on the triangle, and release it at rest, it can't start moving, because there would be no way for it to convert energy of position into energy of motion. Thus the chain must be perfectly balanced. Now by symmetry, the arc of the chain hanging underneath the triangle has equal tension at both ends, so removing this arc wouldn't affect the balance of the rest of the chain. This means that a weight of three units hanging vertically balances a weight of five units hanging diagonally along the hypotenuse.

The mechanical advantage of the inclined plane is therefore `5"/"3`, which is exactly the same as the result, `1"/"sin theta`, that we got on p. 223 by analyzing force vectors. What this shows is that Newton's laws and conservation laws are not logically separate, but rather are very closely related descriptions of nature. In the cases where Newton's laws are true, they give the same answers as the conservation laws. This is an example of a more general idea, called the correspondence principle, about how science progresses over time. When a newer, more general theory is proposed to replace an older theory, the new theory must agree with the old one in the realm of applicability of the old theory, since the old theory only became accepted as a valid theory by being verified experimentally in a variety of experiments. In other words, the new theory must be backward-compatible with the old one. Even though conservation laws can prove things that Newton's laws can't (that perpetual motion is impossible, for example), they aren't going to disprove Newton's laws when applied to mechanical systems where we already knew Newton's laws were valid.

Discussion Question

A   Hydroelectric power (water flowing over a dam to spin turbines) appears to be completely free. Does this violate conservation of energy? If not, then what is the ultimate source of the electrical energy produced by a hydroelectric plant?

B   How does the proof in example 3 fail if the assumption of a frictionless surface doesn't hold?

11.2 Energy by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.