6.4 Summary by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

vCalc Formulary	6.4 Summary
`a_x = F_"x,total"/ m`	x acceleration
`a_y = F_"y,total"/m`	y acceleration
`a_z = F_"z,total"/m`	z acceleration
`v_x= v cos(theta)`	`Velocity_x`
`v_y = v sin(theta)`	`Velocity_y`
`R = ((2v^2)/g) sin(theta) cos(theta)`	Simplified Range

Summary

Vocabulary

component — the part of a velocity, acceleration, or force that would be perceptible to an observer who could only see the universe projected along a certain one-dimensional axis

parabola — the mathematical curve whose graph has `y` proportional to `x^2`

Notation

`x`, `y`, `z` — an object's positions along the `x`, `y`, and `z` axes

`v_x, v_y, v_z` — the `x`, `y`, and `z` components of an object's velocity; the rates of change of the object's `x`, `y`, and `z` coordinates

`a_x, a_y, a_z` — the `x`, `y`, and `z` components of an object's acceleration; the rates of change of `v_x, v_y`, and `v_z`

Summary

A force does not produce any effect on the motion of an object in a perpendicular direction. The most important application of this principle is that the horizontal motion of a projectile has zero acceleration, while the vertical motion has an acceleration equal to `g`. That is, an object's horizontal and vertical motions are independent. The arc of a projectile is a parabola.

Motion in three dimensions is measured using three coordinates, `x`, `y`, and `z`. Each of these coordinates has its own corresponding velocity and acceleration. We say that the velocity and acceleration both have `x`, `y`, and `z` components

Newton's second law is readily extended to three dimensions by rewriting it as three equations predicting the three components of the acceleration,

`a_x=F_"x,total" / m,`
`a_y = F_"y,total"/m`
`a_z = F_"z,total"/m`

and likewise for the first and third laws.

Homework Problems

Key

`sqrt` A computerized answer check is available online. (Search vCalc!)

`int` A problem that requires calculus.

 `***` A difficult problem.

1. (a) A ball is thrown straight up with velocity `v`. Find an equation for the height to which it rises.`sqrt`

(b) Generalize your equation for a ball thrown at an angle `theta` above horizontal, in which case its initial velocity components are `v_x=vcos theta`  and `v_y=vsintheta`.`sqrt`

2. At the 2010 Salinas Lettuce Festival Parade, the Lettuce Queen drops her bouquet while riding on a float moving toward the right. Sketch the shape of its trajectory in her frame of reference, and compare with the shape seen by one of her admirers standing on the sidewalk.

3. Two daredevils, Wendy and Bill, go over Niagara Falls. Wendy sits in an inner tube, and lets the 30 km/hr velocity of the river throw her out horizontally over the falls. Bill paddles a kayak, adding an extra 10 km/hr to his velocity. They go over the edge of the falls at the same moment, side by side. Ignore air friction. Explain your reasoning.
(a) Who hits the bottom first?
(b) What is the horizontal component of Wendy's velocity on impact?
(c) What is the horizontal component of Bill's velocity on impact?
(d) Who is going faster on impact?

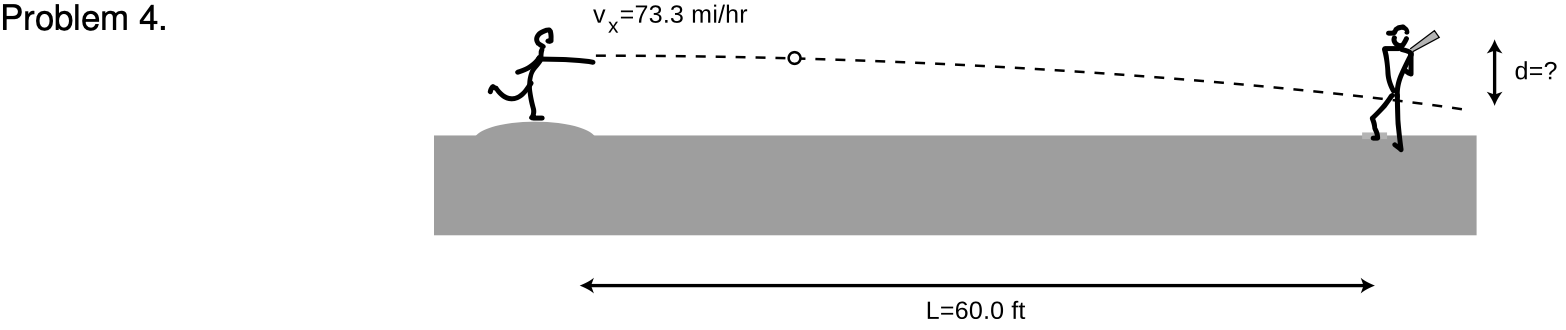
4. A baseball pitcher throws a pitch clocked at `v_x`=`73.3 "mi""/"h`. He throws horizontally. By what amount, `d`, does the ball drop by the time it reaches home plate, `L`=60.0 ft away?
(a) First find a symbolic answer in terms of `L`, `v_x`, and g`. sqrt`
(b) Plug in and find a numerical answer. Express your answer in units of ft. (Note: 1 ft=12 in, 1 mi=5280 ft, and 1 in=2.54 cm)`sqrt`

 

5. A cannon standing on a flat field fires a cannonball with a muzzle velocity `v`, at an angle `theta` above horizontal. The cannonball thus initially has velocity components `v_x= v cos(theta)`and `v_y = v sin(theta)`
(a) Show that the cannon's range (horizontal distance to where the cannonball falls) is given by the equation `R = ((2v^2)/g) sin(theta) cos(theta)`

(b) Interpret your equation in the cases of `theta=0` and `theta=90°`.(solution in the pdf version of the book)

6. Assuming the result of problem 5 for the range of a projectile, `R = ((2v^2)/g) sin(theta) cos(theta)`, show that the maximum range is for `theta=45°`?`int`

7. Two cars go over the same speed bump in a parking lot, Maria's Maserati at 25 miles per hour and Park's Porsche at 37. How many times greater is the vertical acceleration of the Porsche? Hint: Remember that acceleration depends both on how much the velocity changes and on how much time it takes to change. `***`

6.4 Summary by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.