17.1 Period, frequency, and amplitude by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
17.1 Period, frequency, and amplitude
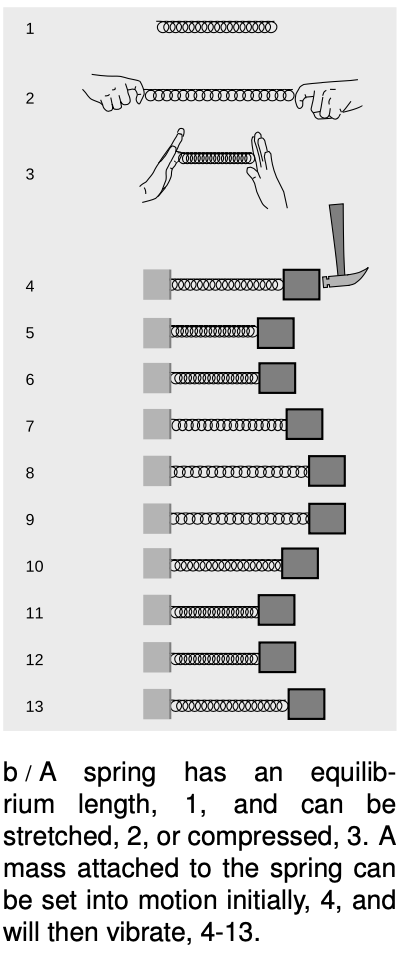Figure b shows our most basic example of a vibration. With no forces on it, the spring assumes its equilibrium length, b1. It can be stretched, 2, or compressed, 3. We attach the spring to a wall on the left and to a mass on the right. If we now hit the mass with a hammer, 4, it oscillates as shown in the series of snapshots, 4-13. If we assume that the mass slides back and forth without friction and that the motion is one-dimensional, then conservation of energy proves that the motion must be repetitive. When the block comes back to its initial position again, 7, its potential energy is the same again, so it must have the same kinetic energy again. The motion is in the opposite direction, however. Finally, at 10, it returns to its initial position with the same kinetic energy and the same direction of motion. The motion has gone through one complete cycle, and will now repeat forever in the absence of friction.
The usual physics terminology for motion that repeats itself over and over is periodic motion, and the time required for one repetition is called the period, `T`. (The symbol `P` is not used because of the possible confusion with momentum.) One complete repetition of the motion is called a cycle.
We are used to referring to short-period sound vibrations as “high” in pitch, and it sounds odd to have to say that high pitches have low periods. It is therefore more common to discuss the rapidity of a vibration in terms of the number of vibrations per second, a quantity called the frequency, `f`. Since the period is the number of seconds per cycle and the frequency is the number of cycles per second, they are reciprocals of each other,
Example 1: A carnival game
In the carnival game shown in figure `d`, the rube is supposed to push the bowling ball on the track just hard enough so that it goes over the hump and into the valley, but does not come back out again. If the only types of energy involved are kinetic and potential, this is impossible.
Suppose you expect the ball to come back to a point such as the one shown with the dashed outline, then stop and turn around. It would already have passed through this point once before, going to the left on its way into the valley. It was moving then, so conservation of energy tells us that it cannot be at rest when it comes back to the same point. The motion that the customer hopes for is physically impossible. There is a physically possible periodic motion in which the ball rolls back and forth, staying confined within the valley, but there is no way to get the ball into that motion beginning from the place where we start. There is a way to beat the game, though. If you put enough spin on the ball, you can create enough kinetic friction so that a significant amount of heat is generated. Conservation of energy then allows the ball to be at rest when it comes back to a point like the outlined one, because kinetic energy has been converted into heat.
Example 2: Period and frequency of a fly's wing-beats
A Victorian parlor trick was to listen to the pitch of a fly's buzz, reproduce the musical note on the piano, and announce how many times the fly's wings had flapped in one second. If the fly's wings flap, say, 200 times in one second, then the frequency of their motion is `f`=200/1`s`=200 `s^-1`. The period is one 200th of a second, `f=1/T`=(1/200) s=0.005 `s`.
Units of inverse second, `s^(-1)`, are awkward in speech, so an abbreviation has been created. One Hertz, named in honor of a pioneer of radio technology, is one cycle per second. In abbreviated form, `1 Hz`=`s^(-1)`. This is the familiar unit used for the frequencies on the radio dial.
Example 3: Frequency of a radio station
`Delta`KKJZ's frequency is 88.1 MHz. What does this mean, and what period does this correspond to?
`Delta` The metric prefix M- is mega-, i.e., millions. The radio waves emitted by KKJZ's transmitting antenna vibrate 88.1 million times per second. This corresponds to a period of
`f=1/T`=`1.14×10^(-8) s`
This example shows a second reason why we normally speak in terms of frequency rather than period: it would be painful to have to refer to such small time intervals routinely. I could abbreviate by telling people that KKJZ's period was 11.4 nanoseconds, but most people are more familiar with the big metric prefixes than with the small ones.
Units of frequency are also commonly used to specify the speeds of computers. The idea is that all the little circuits on a computer chip are synchronized by the very fast ticks of an electronic clock, so that the circuits can all cooperate on a task without getting ahead or behind. Adding two numbers might require, say, 30 clock cycles. Microcomputers these days operate at clock frequencies of about a gigahertz.
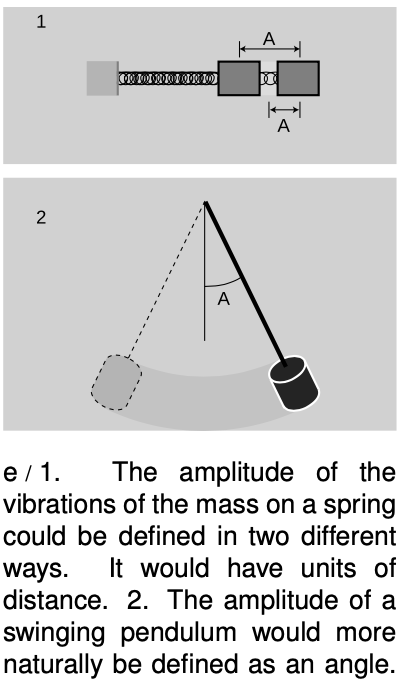
We have discussed how to measure how fast something vibrates, but not how big the vibrations are. The general term for this is amplitude, `A`. The definition of amplitude depends on the system being discussed, and two people discussing the same system may not even use the same definition. In the example of the block on the end of the spring, `e`/`1`, the amplitude will be measured in distance units such as cm. One could work in terms of the distance traveled by the block from the extreme left to the extreme right, but it would be somewhat more common in physics to use the distance from the center to one extreme. The former is usually referred to as the peak-to-peak amplitude, since the extremes of the motion look like mountain peaks or upside-down mountain peaks on a graph of position versus time.
In other situations we would not even use the same units for amplitude. The amplitude of a child on a swing, or a pendulum, `e`/2, would most conveniently be measured as an angle, not a distance, since her feet will move a greater distance than her head. The electrical vibrations in a radio receiver would be measured in electrical units such as volts or amperes.
17.1 Period, frequency, and amplitude by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.