LM 31.3 The lensmaker's equation Collection

31.3 The lensmaker's equation by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

31.3 The lensmaker's equation (optional)

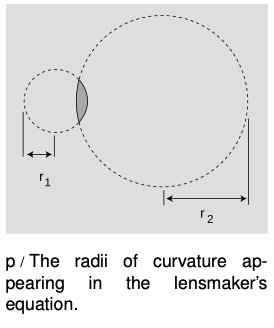The focal length of a spherical mirror is simply `r"/"2`, but we cannot expect the focal length of a lens to be given by pure geometry, since it also depends on the index of refraction of the lens. Suppose we have a lens whose front and back surfaces are both spherical. (This is no great loss of generality, since any surface with a sufficiently shallow curvature can be approximated with a sphere.) Then if the lens is immersed in a medium with an index of refraction of 1, its focal length is given approximately by

`f=[(n-1)|1/r_1+-1/r_2|]^(-1)`,

where `n` is the index of refraction and `r_1` and `r_2` are the radii of curvature of the two surfaces of the lens. This is known as the lensmaker's equation. In my opinion it is not particularly worthy of memorization. The positive sign is used when both surfaces are curved outward or both are curved inward; otherwise a negative sign applies. The proof of this equation is left as an exercise to those readers who are sufficiently brave and motivated.

31.3 The lensmaker's equation by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.