Quantcast
Loading [MathJax]/jax/output/CommonHTML/jax.js

Area of Circle Within a Triangle

vCalc Reviewed
A=π⋅(√a+b+c2(a+b+c2-a)(a+b+c2-b)(a+b+c2-c)a+b+c2)2
(a)Length Side a
(b)Length Side b
(c)Length Side c

The Area of Circle Within a Triangle calculator computes the area (blue circle in diagram) of circle that is perfectly inscribed within a triangle.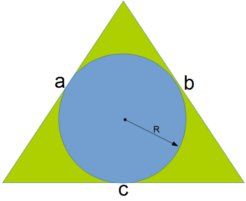

INSTRUCTIONS: Choose units and enter the following:

  • (a) Length of Side a
  • (b) Length of Side b
  • (c) Length of Side c

Area of Circle Within a Triangle (A): The area is returned in square meters and the radius (r) is returned in meters.  However, these can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The formula for  Area of Circle Within a Triangle equation is:

A= π⋅(√a+b+c2(a+b+c2-a)(a+b+c2-b)(a+b+c2-c) a+b+c2)2

where:

  • A = Area of Circle inscribe within a triangle.
  • a = length of side a
  • b = length of side b
  • c = length of side c

Note: (a+b+c)/2 is the semi-perimeter of the triangle

A triangle is a polygon with three sides, three vertices (corners), and three angles. Triangles can be classified based on the lengths of their sides and the measures of their angles as follows:

By Side Lengths:

  • Equilateral Triangle: All three sides are equal in length.
  • Isosceles Triangle: Two sides are equal in length.
  • Scalene Triangle: All three sides have different lengths.

By Angle Measures:

  • Acute Triangle: All three angles are less than 90 degrees.
  • Right Triangle: One angle is exactly 90 degrees.
  • Obtuse Triangle: One angle is greater than 90 degrees.

The sum of the interior angles of any triangle always adds up to 180 degrees. 

Triangle Calculators