The Area of a Triangle Area based on Two Sides and Angle calculator 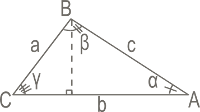 computes the area of a triangle given the length of two sides (b & c) and the inscribed angle (α).
computes the area of a triangle given the length of two sides (b & c) and the inscribed angle (α).
INSTRUCTIONS: Choose units and enter the following:
- (α) Angle between Two Sides
- (b) Length of Side
- (c) Length of other Side
AREA (A):The calculator returns the area in square meters (m²). However, this can be automatically converted to other area units (e.g. square feet) via the pull-down menu.
The Math / Science
The formula for the area of a triangle based on the length of two sides and the angle between them is:
`A = 1/2*b*c*sin(α)`
where:
- A = Area of the triangle
- b = length of one side
- c = length of other side
- α = angle between them
A triangle is a polygon with three sides, three vertices (corners), and three angles. Triangles can be classified based on the lengths of their sides and the measures of their angles as follows:
By Side Lengths:
- Equilateral Triangle: All three sides are equal in length.
- Isosceles Triangle: Two sides are equal in length.
- Scalene Triangle: All three sides have different lengths.
By Angle Measures:
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
The sum of the interior angles of any triangle always adds up to 180 degrees.
Triangle Calculators
- Area of Triangle (base and height)
- Area of Triangle (two sides and interior angle)
- Area of Triangle (two angles and interior side)
- Area of Triangle (three sides)
- Area of Equilateral Triangle
- Area of Triangle (three points)
- Height of Triangle
- Width of Triangle
- Triangle Perimeter
- Interior Angle of a triangle based on the length of three sides
- Semi-perimeter of a triangle
- Area of Circle Within a Triangle
- Area of Circle Around a Triangle
- Area between two vectors
- Triangle Volume