The half-life of a chemical reaction is defined as the time required for half the amount of a reactant to be converted into product. To find the half-lives of different order reactions, we use integrated rate laws and rate constants to relate concentration to time. There are three different rate laws that can be used to find the half-life of a chemical reaction.
Zero Order
For zero order kinetics, the half-life is not dependent on the concentration of the substance. In other words, rate = k. This means that no matter how much substrate is added, and no matter how high of a concentration is present in solution, the rate of the reaction will not increase. A graphical representation of this would show linear data with a negative slope, as shown in the image below. The rate law for a zero order reaction is [A] = [A]0 - kt. To find the half-life for a zero order reaction, the equation t1/2 = [A]0 / 2k is used.
Where
- k is the temperature-dependent reaction rate constant
- t1/2 is the half-life
- [A]0 is the initial concentration
First Order
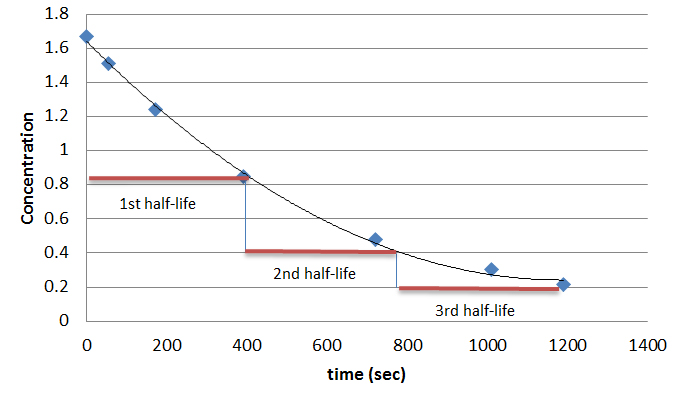
First order reactions are dependent on concentration; meaning the more substrate added, the faster the reaction will proceed. The rate for this order is rate = k[A]. First order reactions have unique graphs, such as the one below. Notice how it takes the same amount of time for the concentration to decrease between points. The rate law for a first order reaction is [A] = [A]0e-kt. To find the half-life for a first order reaction, the equation t1/2 = 0.693 / k is used.
Where
- k is the temperature-dependent reaction rate constant
- t1/2 is the half-life
Second Order
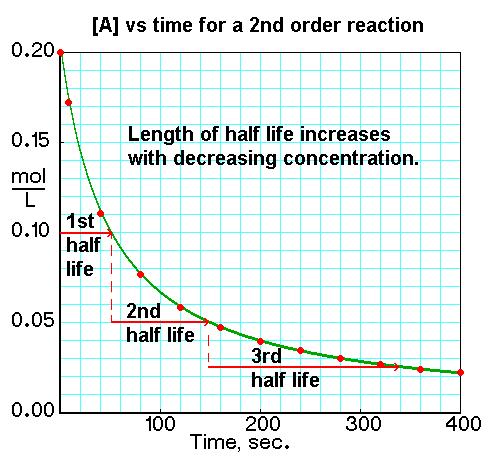
Second order reactions are dependent on concentration, just like first order reactions; however, second order reactions react much faster than first order. The rate for second order reactions is rate = k[A]2, so it decreases exponentially, unlike first order reactions. The rate law is 1/[A] = kt + 1/[A]0 and the equation used to find the half-life of a second order reaction is t1/2 = 1 / k[A]0.
Where
- k is the temperature-dependent reaction rate constant
- t1/2 is the half life
- [A]0 is the initial concentration
References
Whitten, et al. "Chemistry" 10th Edition. Pp. 626-631