Half-Life (first order)

The First Order Half-Life calculator computes the first order half-life based on the temperature dependent rate constant.

INSTRUCTIONS: Enter the following:

• (k) Temperature dependent reaction rate constant.

Half Life (t_½): The calculator returns the half-life in seconds.  However this can be automatically converted to compatible units via the pull-down menu.

Chemistry Rate Law Calculators

• Zero Order Rate Law (Integral form)
• Zero Order  Half Life
• Zero Order Rate Law
• First Order Rate Law (Integral form)
• First Order Half Life
• First Order Rate Law
• Second Order Rate Law (Integral form)
• Second Order Half Life
• Second Order Rate Law

The Math / Science

The half-life of a chemical reaction is defined as the time required for half the amount of a reactant to be converted into product. To find the half-lives of different order reactions, we use integrated rate laws and rate constants to relate concentration to time. There are three different rate laws that can be used to find the half-life of a chemical reaction: zero, first, and second order.

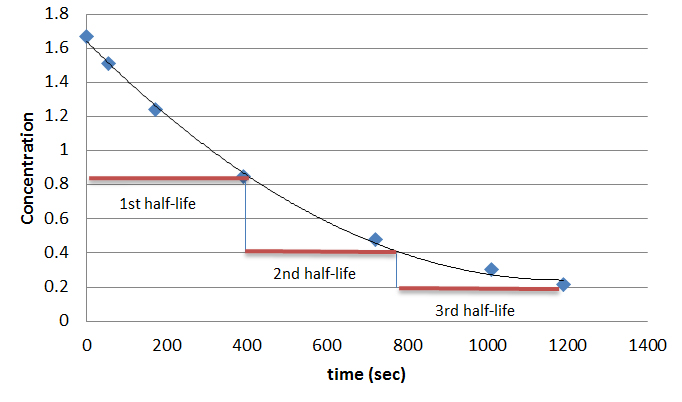
First order reactions are dependent on concentration; meaning the more substrate added, the faster the reaction will proceed. The rate for this order is rate = k[A]. First order reactions have unique graphs, such as the one below. Notice how it takes the same amount of time for the concentration to decrease between points. The rate law for a first order reaction is [A] = [A]₀e^-kt. The formula for half-life for a first order reaction is:

t_1/2 = 0.693 / k 

• t_1/2 = first order half-life
• k is the temperature-dependent reaction rate constant
• t_1/2 is the half-life

References

ChemWiki

Whitten, et al. "Chemistry" 10th Edition. Pp. 626

See Also

Rate Law Half-Lives

Half-life (zero order)

Half-life (second order)