31.1 Refraction  by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

31.1 Refraction

Refraction

The fundamental physical phenomenon at work in the eye is that when light crosses a boundary between two media (such as air and the eye's jelly), part of its energy is reflected, but part passes into the new medium. In the ray model of light, we describe the original ray as splitting into a reflected ray and a transmitted one (the one that gets through the boundary). Of course the reflected ray goes in a direction that is different from that of the original one, according to the rules of reflection we have already studied. More surprisingly --- and this is the 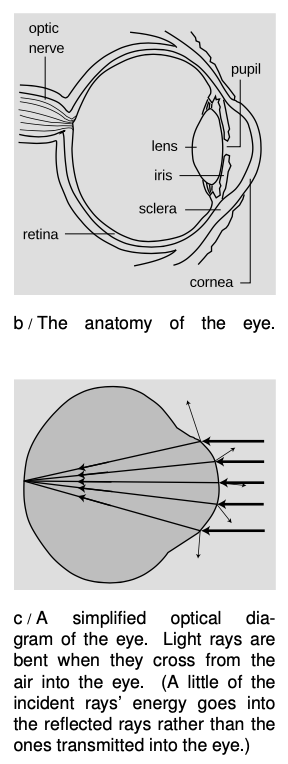crucial point for making your eye focus light --- the transmitted ray is bent somewhat as well. This bending phenomenon is called refraction. The origin of the word is the same as that of the word “fracture,” i.e., the ray is bent or “broken.” (Keep in mind, however, that light rays are not physical objects that can really be “broken.”) Refraction occurs with all waves, not just light waves.

The actual anatomy of the eye, b, is quite complex, but in essence it is very much like every other optical device based on refraction. The rays are bent when they pass through the front surface of the eye, c. Rays that enter farther from the central axis are bent more, with the result that an image is formed on the retina. There is only one slightly novel aspect of the situation. In most human-built optical devices, such as a movie projector, the light is bent as it passes into a lens, bent again as it reemerges, and then reaches a focus beyond the lens. In the eye, however, the “screen” is inside the eye, so the rays are only refracted once, on entering the jelly, and never emerge again.

A common misconception is that the “lens” of the eye is what does the focusing. All the transparent parts of the eye are made of fairly similar stuff, so the dramatic change in medium is when a ray crosses from the air into the eye (at the outside surface of the cornea). This is where nearly all the refraction takes place. The lens medium differs only slightly in its optical properties from the rest of the eye, so very little refraction occurs as light enters and exits the lens. The lens, whose shape is adjusted by muscles attached to it, is only meant for fine-tuning the focus to form images of near or far objects.

Refractive properties of media

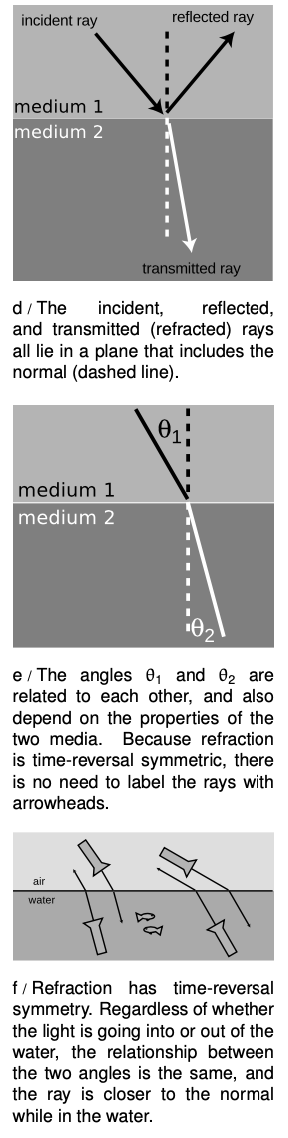
What are the rules governing refraction? The first thing to observe is that just as with reflection, the new, bent part of the ray lies in the same plane as the normal (perpendicular) and the incident ray, d.

If you try shooting a beam of light at the boundary between two substances, say water and air, you'll find that regardless of the angle at which you send in the beam, the part of the beam in the water is always closer to the normal line, e. It doesn't matter if the ray is entering the water or leaving, so refraction is symmetric with respect to time-reversal, f.

If, instead of water and air, you try another combination of substances, say plastic and gasoline, again you'll find that the ray's angle with respect to the normal is consistently smaller in one and larger in the other. Also, we find that if substance A has rays closer to normal than in B, and B has rays closer to normal than in C, then A has rays closer to normal than C. This means that we can rank-order all materials according to their refractive properties. Isaac Newton did so, including in his list many amusing substances, such as “Danzig vitriol” and “a pseudo-topazius, being a natural, pellucid, brittle, hairy stone, of a yellow color.” Several general rules can be inferred from such a list:

• Vacuum lies at one end of the list. In refraction across the interface between vacuum and any other medium, the other medium has rays closer to the normal.
• Among gases, the ray gets closer to the normal if you increase the density of the gas by pressurizing it more.
• The refractive properties of liquid mixtures and solutions vary in a smooth and systematic manner as the proportions of the mixture are changed.
• Denser substances usually, but not always, have rays closer to the normal.

The second and third rules provide us with a method for measuring the density of an unknown sample of gas, or the concentration of a solution. The latter technique is very commonly used, and the CRC Handbook of Physics and Chemistry, for instance, contains extensive tables of the refractive properties of sugar solutions, cat urine, and so on.

Snell's law

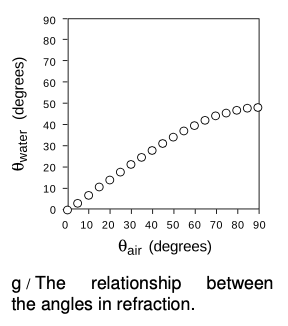The numerical rule governing refraction was discovered by Snell, who must have collected experimental data something like what is shown on this graph and then attempted by trial and error to find the right equation. The equation he came up with was

`(sintheta_1)/(sintheta_2)="constant"`.

The value of the constant would depend on the combination of media used. For instance, any one of the data points in the graph would have sufficed to show that the constant was 1.3 for an air-water interface (taking air to be substance 1 and water to be substance 2).

Snell further found that if media A and B gave a constant `K_(AB)` and media `B` and `C` gave a constant `K_(BC)`, then refraction at an interface between `A` and `C` would be described by a constant equal to the product, `K_(AC)=K_(AB)K_(BC)`. This is exactly what one would expect if the constant depended on the ratio of some number characterizing one medium to the number characteristic of the second medium. This number is called the index of refraction of the medium, written as `n` in equations. Since measuring the angles would only allow him to determine the ratio of the indices of refraction of two media, Snell had to pick some medium and define it as having `n=1`. He chose to define vacuum as having `n=1`. (The index of refraction of air at normal atmospheric pressure is 1.0003, so for most purposes it is a good approximation to assume that air has `n=1`.) He also had to decide which way to define the ratio, and he chose to define it so that media with their rays closer to the normal would have larger indices of refraction. This had the advantage that denser media would typically have higher indices of refraction, and for this reason the index of refraction is also referred to as the optical density. Written in terms of indices of refraction, Snell's equation becomes

`(sin theta_1)/(sin theta_2)=n_2/n_1,`

but rewriting it in the form

`n_1sin theta_1=n_2sin theta_2`

[relationship between angles of rays at the interface between media with indices of refraction `n_1` and `n_2`; angles are defined with respect to the normal] makes us less likely to get the 1's and 2's mixed up, so this the way most people remember Snell's law. A few indices of refraction are given in the back of the book.

self-check:

(1) What would the graph look like for two substances with the same index of refraction?

(2) Based on the graph, when does refraction at an air-water interface change the direction of a ray most strongly?

(answer in the back of the PDF version of the book)

Example 1: Finding an angle using Snell's law

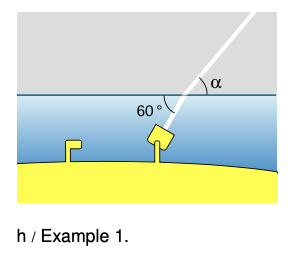`=>` A submarine shines its searchlight up toward the surface of the water. What is the angle `alpha` shown in the figure?

`=>` The tricky part is that Snell's law refers to the angles with respect to the normal. Forgetting this is a very common mistake. The beam is at an angle of `30°` with respect to the normal in the water. Let's refer to the air as medium 1 and the water as 2. Solving Snell's law for `theta_1`, we find

[Private Equation].

As mentioned above, air has an index of refraction very close to 1, and water's is about 1.3, so we find `theta_1=40°`. The angle `alpha` is therefore `50°`.

The index of refraction is related to the speed of light.

What neither Snell nor Newton knew was that there is a very simple interpretation of the index of refraction. This may come as a relief to the reader who is taken aback by the complex reasoning involving proportionalities that led to its definition. Later experiments showed that the index of refraction of a medium was inversely proportional to the speed of light in that medium. Since `c` is defined as the speed of light in vacuum, and `n=1` is defined as the index of refraction of vacuum, we have

[Private Equation].

[`n= ` medium's index of refraction, `v=` speed of light in that medium, `c=` speed of light in a vacuum]

Many textbooks start with this as the definition of the index of refraction, although that approach makes the quantity's name somewhat of a mystery, and leaves students wondering why `c"/"v` was used rather than `v"/"c`. It should also be noted that measuring angles of refraction is a far more practical method for determining `n` than direct measurement of the speed of light in the substance of interest.

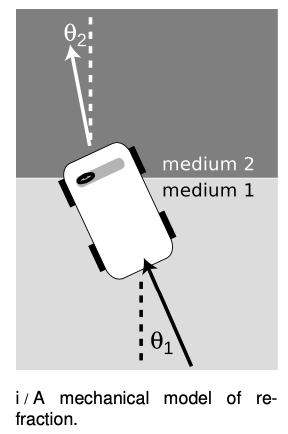A mechanical model of Snell's law

Why should refraction be related to the speed of light? The mechanical model shown in the figure may help to make this more plausible. Suppose medium 2 is thick, sticky mud, which slows down the car. The car's right wheel hits the mud first, causing the right side of the car to slow down. This will cause the car to turn to the right until is moves far enough forward for the left wheel to cross into the mud. After that, the two sides of the car will once again be moving at the same speed, and the car will go straight.

Of course, light isn't a car. Why should a beam of light have anything resembling a “left wheel” and “right wheel?” After all, the mechanical model would predict that a motorcycle would go straight, and a motorcycle seems like a better approximation to a ray of light than a car. The whole thing is just a model, not a description of physical reality.

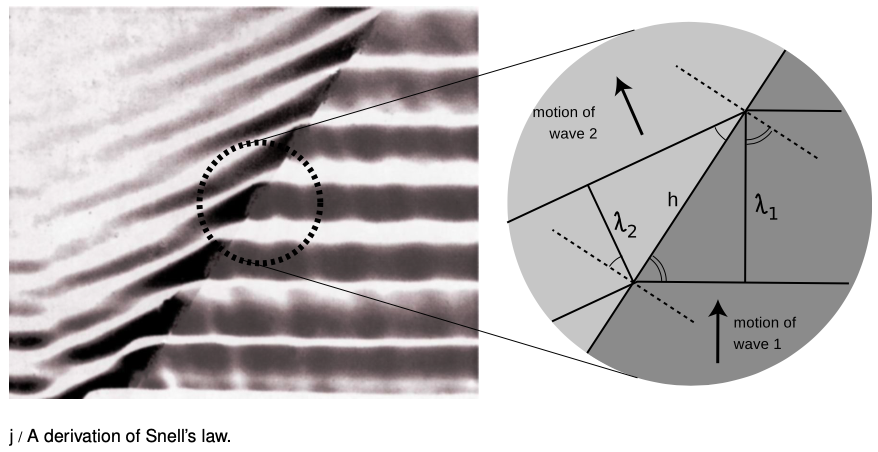
A derivation of Snell's law

However intuitively appealing the mechanical model may be, light is a wave, and we should be using wave models to describe refraction. In fact Snell's law can be derived quite simply from wave concepts. Figure j shows the refraction of a water wave. The water in the upper left part of the tank is shallower, so the speed of the waves is slower there, and their wavelengths is shorter. The reflected part of the wave is also very faintly visible.

In the close-up view on the right, the dashed lines are normals to the interface. The two marked angles on the right side are both equal to `theta_1`, and the two on the left to `theta_2`.

Trigonometry gives

`sin theta_1=lambda_1"/"h` and
`sin theta_2=lambda_2"/"h`.

Eliminating `h` by dividing the equations, we find

`(sin theta_1)/(sin theta_2)=lambda_1/lambda_2`.

The frequencies of the two waves must be equal or else they would get out of step, so by `v=flambda` we know that their wavelengths are proportional to their velocities. Combining `lambdapropv` with `vprop1"/"n` gives `lambdaprop1"/"n`, so we find

`(sin theta_1)/(sin theta_2)=n_2/n_1`,

which is one form of Snell's law.

Example 2: Ocean waves near and far from shore

Ocean waves are formed by winds, typically on the open sea, and the wavefronts are perpendicular to the direction of the wind that formed them. At the beach, however, you have undoubtedly observed that waves tend come in with their wavefronts very nearly (but not exactly) parallel to the shoreline. This is because the speed of water waves in shallow water depends on depth: the shallower the water, the slower the wave. Although the change from the fast-wave region to the slow-wave region is gradual rather than abrupt, there is still refraction, and the wave motion is nearly perpendicular to the normal in the slow region.

Color and refraction

In general, the speed of light in a medium depends both on the medium and on the wavelength of the light. Another way of saying it is that a medium's index of refraction varies with wavelength. This is why a prism can be used to split up a beam of white light into a rainbow. Each wavelength of light is refracted through a different angle.

How much light is reflected, and how much is transmitted?

In chapter 20 we developed an equation for the percentage of the wave energy that is transmitted and the percentage reflected at a boundary between media. This was only done in the case of waves in one dimension, however, and rather than discuss the full three dimensional generalization it will be more useful to go into some qualitative observations about what happens. First, reflection happens only at the interface between two media, and two media with the same index of refraction act as if they were a single medium. Thus, at the interface between media with the same index of refraction, there is no reflection, and the ray keeps going straight. Continuing this line of thought, it is not surprising that we observe very little reflection at an interface between media with similar indices of refraction.

The next thing to note is that it is possible to have situations where no possible angle for the refracted ray can satisfy Snell's law. Solving Snell's law for `theta_2`, we find

[Private Equation],

and if `n_1` is greater than `n_2`, then there will be large values of `theta_1` for which the quantity `(n_1/n_2)sin theta` is greater than one, meaning that your calculator will flash an error message at you when you try to take the inverse sine. What can happen physically in such a situation? The answer is that all the light is reflected, so there is no refracted ray. This phenomenon is known as total internal reflection, and is used in the fiber-optic cables that nowadays carry almost all long-distance telephone calls. The electrical signals from your phone travel to a switching center, where they are converted from electricity into light. From there, the light is sent across the country in a thin transparent fiber. The light is aimed straight into the end of the fiber, and as long as the fiber never goes through any turns that are too sharp, the light will always encounter the edge of the fiber at an angle sufficiently oblique to give total internal reflection. If the fiber-optic cable is thick enough, one can see an image at one end of whatever the other end is pointed at.

Alternatively, a bundle of cables can be used, since a single thick cable is too hard to bend. This technique for seeing around corners is useful for making surgery less traumatic. Instead of cutting a person wide open, a surgeon can make a small “keyhole” incision and insert a bundle of fiber-optic cable (known as an endoscope) into the body.

Since rays at sufficiently large angles with respect to the normal may be completely reflected, it is not surprising that the relative amount of reflection changes depending on the angle of incidence, and is greatest for large angles of incidence.

Discussion Questions

A   What index of refraction should a fish have in order to be invisible to other fish?

B   Does a surgeon using an endoscope need a source of light inside the body cavity? If so, how could this be done without inserting a light bulb through the incision?

C   A denser sample of a gas has a higher index of refraction than a less dense sample (i.e., a sample under lower pressure), but why would it not make sense for the index of refraction of a gas to be proportional to density?

D   The earth's atmosphere gets thinner and thinner as you go higher in altitude. If a ray of light comes from a star that is below the zenith, what will happen to it as it comes into the earth's atmosphere?

E   Does total internal reflection occur when light in a denser medium encounters a less dense medium, or the other way around? Or can it occur in either case?

31.1 Refraction  by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.