13.3 Varying force by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
13.3 Varying force
Up until now we have done no actual calculations of work in cases where the force was not constant. The question of how to treat such cases is mathematically analogous to the issue of how to generalize the equation (distance)=(velocity)(time) to cases where the velocity was not constant. There, we found that the correct generalization was to find the area under the graph of velocity versus time. The equivalent thing can be done with work:
general rule for calculating work
The work done by a force `F` equals the area under the curve on a graph of `F_(?)` versus `x`. (Some ambiguities are encountered in cases such as kinetic friction.)
The examples in this section are ones in which the force is varying, but is always along the same line as the motion, so `F` is the same as `F_(?)`.
self-check:
In which of the following examples would it be OK to calculate work using , and in which ones would you have to use the area under the `F-x` graph?
(a) A fishing boat cruises with a net dragging behind it.
(b) A magnet leaps onto a refrigerator from a distance.
(c) Earth's gravity does work on an outward-bound space probe.
(answer in the back of the PDF version of the book)
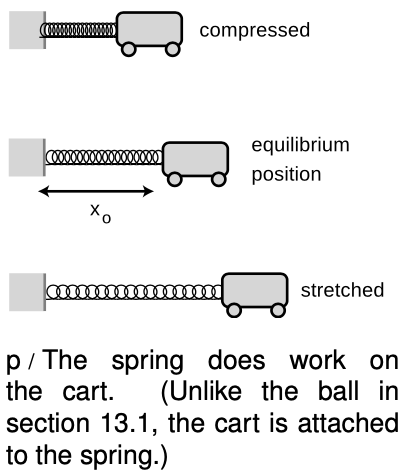
An important and straightforward example is the calculation of the work done by a spring that obeys Hooke's law,
The minus sign is because this is the force being exerted by the spring, not the force that would have to act on the spring to keep it at this position. That is, if the position of the cart in figure p is to the right of equilibrium, the spring pulls back to the left, and vice-versa.
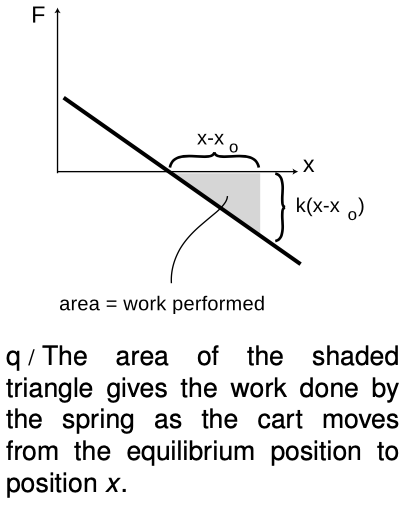
We calculate the work done when the spring is initially at equilibrium and then decelerates the car as the car moves to the right. The work done by the spring on the cart equals the minus area of the shaded triangle, because the triangle hangs below the `x` axis. The area of a triangle is half its base multiplied by its height, so
`W=-1/2k(x-x_o)^2.`
This is the amount of kinetic energy lost by the cart as the spring decelerates it.
It was straightforward to calculate the work done by the spring in this case because the graph of `F` versus `x` was a straight line, giving a triangular area. But if the curve had not been so geometrically simple, it might not have been possible to find a simple equation for the work done, or an equation might have been derivable only using calculus. Optional section 13.4 gives an important example of such an application of calculus.
Example 5: Energy production in the sun
The sun produces energy through nuclear reactions in which nuclei collide and stick together. The figure depicts one such reaction, in which a single proton (hydrogen nucleus) collides with a carbon nucleus, consisting of six protons and six neutrons. Neutrons and protons attract other neutrons and protons via the strong nuclear force, so as the proton approaches the carbon nucleus it is accelerated. In the language of energy, we say that it loses nuclear potential energy and gains kinetic energy. Together, the seven protons and six neutrons make a nitrogen nucleus. Within the newly put-together nucleus, the neutrons and protons are continually colliding, and the new proton's extra kinetic energy is rapidly shared out among all the neutrons and protons. Soon afterward, the nucleus calms down by releasing some energy in the form of a gamma ray, which helps to heat the sun.
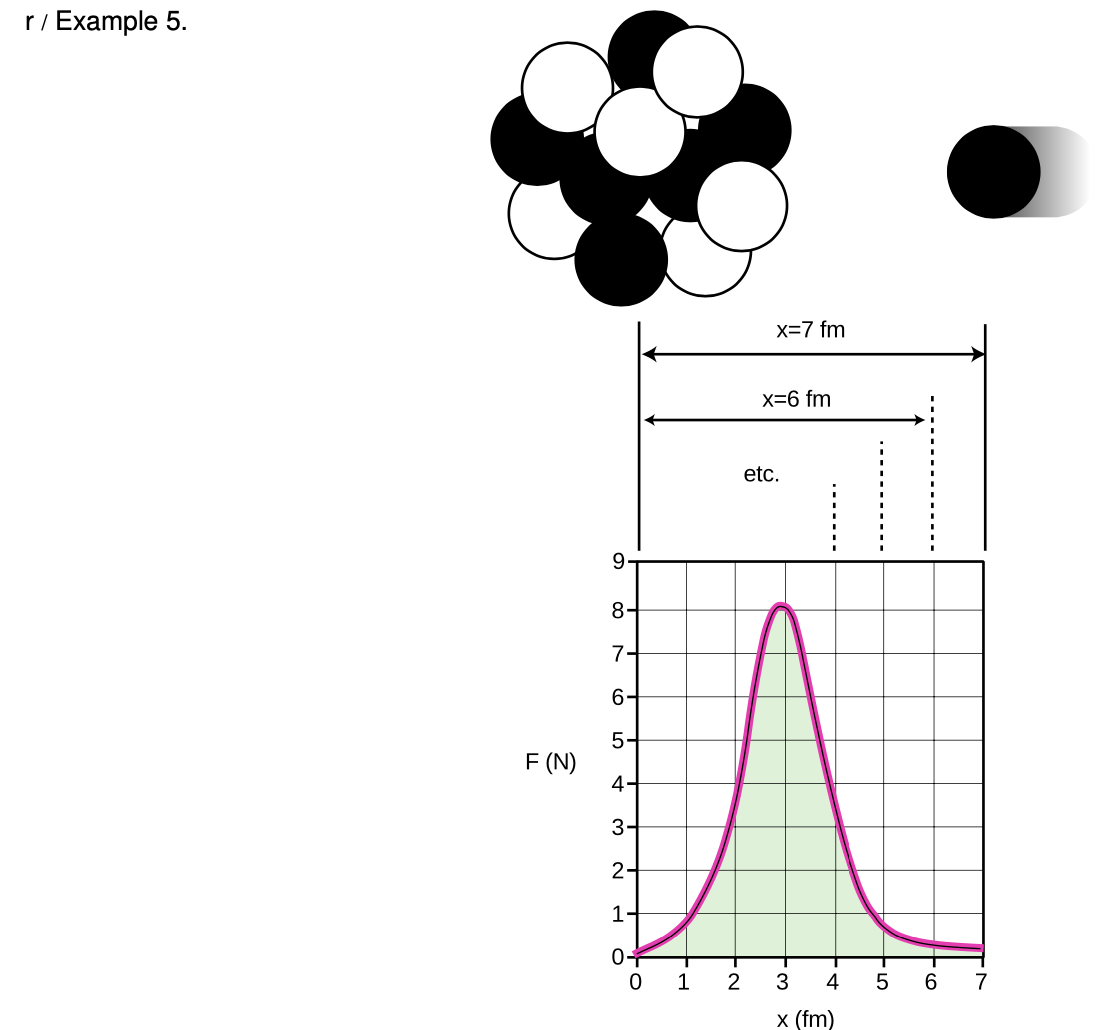
The graph shows the force between the carbon nucleus and the proton as the proton is on its way in, with the distance in units of femtometers (`1 " fm"=10^(-15) "m"`). Amusingly, the force turns out to be a few newtons: on the same order of magnitude as the forces we encounter ordinarily on the human scale. Keep in mind, however, that a force this big exerted on a single subatomic particle such as a proton will produce a truly fantastic acceleration (on the order of `10^27 m"/"s^2`!).
Why does the force have a peak around `x=3 " fm"`, and become smaller once the proton has actually merged with the nucleus? At `x=3 " fm"`, the proton is at the edge of the crowd of protons and neutrons. It feels many attractive forces from the left, and none from the right. The forces add up to a large value. However if it later finds itself at the center of the nucleus, `x=0`, there are forces pulling it from all directions, and these force vectors cancel out.
We can now calculate the energy released in this reaction by using the area under the graph to determine the amount of mechanical work done by the carbon nucleus on the proton. (For simplicity, we assume that the proton came in “aimed” at the center of the nucleus, and we ignore the fact that it has to shove some neutrons and protons out of the way in order to get there.) The area under the curve is about 17 squares, and the work represented by each square is
`(1 N)(10^(-15) m)=10^(-15) J,`
so the total energy released is about
`(10^(-15) J"/""square")(17 "squares")=1.7×10^(-14) J.`
This may not seem like much, but remember that this is only a reaction between the nuclei of two out of the zillions of atoms in the sun. For comparison, a typical chemical reaction between two atoms might transform on the order of `10^(-19)` J of electrical potential energy into heat `-`100,000 times less energy!
As a final note, you may wonder why reactions such as these only occur in the sun. The reason is that there is a repulsive electrical force between nuclei. When two nuclei are close together, the electrical forces are typically about a million times weaker than the nuclear forces, but the nuclear forces fall off much more quickly with distance than the electrical forces, so the electrical force is the dominant one at longer ranges. The sun is a very hot gas, so the random motion of its atoms is extremely rapid, and a collision between two atoms is sometimes violent enough to overcome this initial electrical repulsion.
13.3 Varying force by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.