Quaternion Calculators
The Quaternion Calculator includes functions associated with quaternion mathematics. The quaternions are in the form of "scalar first" (q4,q1,q2,q3). The quaternion arithmetic functions include the following:
- Quaternion Addition
- Quaternion Subtraction
- Quaternion Multiplication
- Quaternion Dot Product
- Quaternion Magnitude
- Quaternion Versor
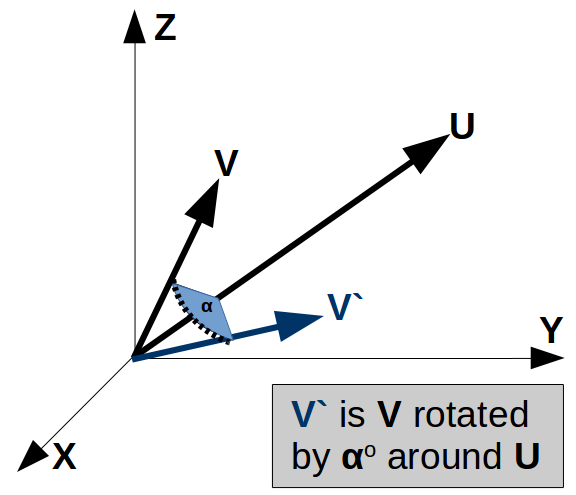 QUATERNION ROTATIONS
QUATERNION ROTATIONS - Quaternion Conjugate
- Quaternion Inverse
- Quaternion of Rotation
- Quaternion to Roll, Pitch and Yaw (Euler Angles)
- Roll, Pitch and Yaw (Euler Angles) to Quaternion
- Vector Rotation
Quaternions
Quaternions can be represented in several ways. One of the ways is similar to the way complex numbers are represented:
q ≡ q4 + q1i + q2j + q3k,
in which q1 , q2 , q3 and q4 , are real numbers, and i, j, and k, are unit “vectors” which obey similar rules to the vectors of the same names found in vector analysis, but with an additional similarity to the i of complex arithmetic which equals `sqrt(-1)` . The multiplication rules for i , j , and k are depicted
conceptually as follows: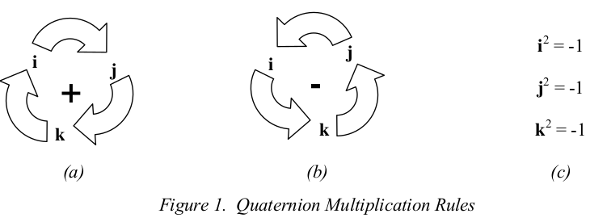
That is, i j = + k, j k = + i, etc. , from figure 1(a) , and j i = - k, i k = -j , etc., from figure 1(b) . Expressed
in this form, the multiplication rules are very easy to remember. Note that the cross products of i, j , and
k obey the rules of vector cross product multiplication, where, for example, given the orthogonal axes,
x, y, and z: x × y = z, y × z = x , and z × x = y .
Note: Quaternions are not commutative, and the following should be noted:
q1*q2 ≠ q2 * q1
q1*q2 ≠ -q2 * q1, but
(q1 * q2) * q3 = q1 * (q2 * q3)
Use of Quaternions in Aerospace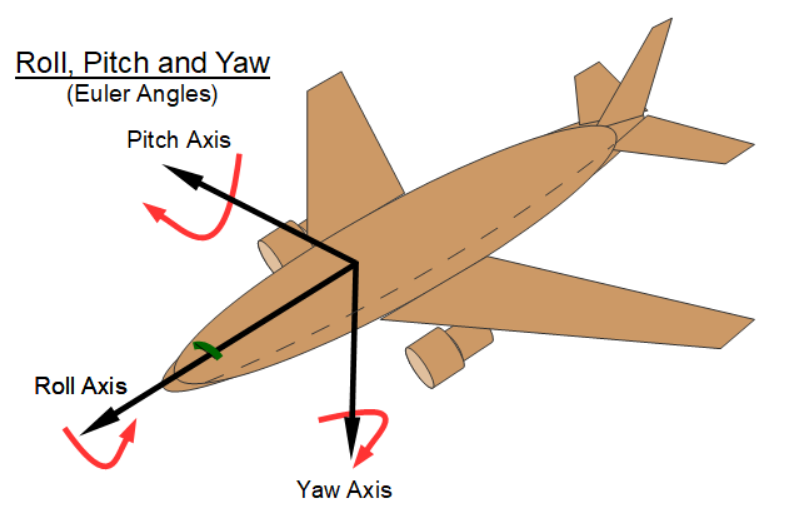
Quaternions are very good for defining the rotation between two coordinate frames. For this reason, time tagged quaternions are used to indicate the attitude (orientation) of a satellite at a specific moment. With an attitude quaternion, satellite mission planners can determine the rotations it takes to go from one attitude to another. This is how sensors on board of satellites are modeled and moved. The same is true for other fixed components such as solar arrays and communication antennae.
