The Mass of a Bottle calculator computes the mass based on the dimensions of the bottle and the mean density of the material. 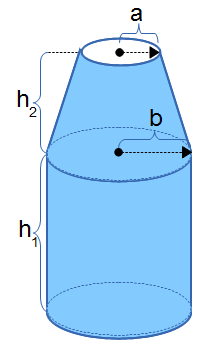
INSTRUCTIONS: Choose the length units you wish (e.g. centimeters or inches) and enter the following:
- (a) neck radius at the top of the bottle
- (h2) height of the tapered neck section
- (b) base section's radius
- (h1) height of the bottle's base that is a constant diameter along it's length from the bottom base to the beginning of the taper.
- (mD) mean density of material.
Mass of the Bottle (M): The calculator returns the mass in grams. However, this can be automatically converted to compatible units via the pull-down menu.
Bottle Calculators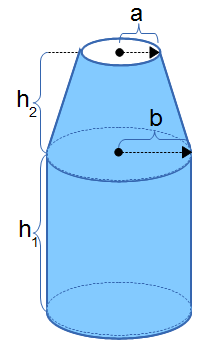
- Surface Area of a Bottle: This computes the surface area of a bottle shaped object based on the dimensions.
- Mass of the Contents of a Bottle: This computes the weight or mass of a bottle shaped object based on the dimensions and the density of its contents.
- Volume of a Bottle: This computes the volume of a bottle shaped object based on the dimensions.
- Bottle Coating Amount: This computes the volume of material needed to coat the surface area of a bottle shaped object.
The Math / Science
The formula for the mass of a bottle shaped object is the volume of the bottle times the density of the material. Assuming normal gravity, this also provides the weight. Geometrically, a bottle shaped object is the combination of right circular cone with a frustum defined by base radius (a) and top radius (b) and height (h2) in between and a cylinder of radius (b) and height (h1). The volume is calculated and then multiplied by a mean density (mD) to provide the mass of the shape. See diagram. KEY WORDS: container
| Common Mean Densities |
|
Natural
Food
Industrial
Fuels
|
Mean Density of Fluids
Mean density is the average amount of mass within a volume for a substance. Note, volume of a material is often highly subject to the temperatures, since materials expand as they warm. For that reason, mean densities of substances are often cited with a set of nominal conditions such as temperature and barometric pressure.
The formula for mean density is:
μD = V / m
where:
- μD = mean density
- V = Volume in units like gallons or liters
- m = Mass in units like kilograms or pounds
Mean density is also often indicated as the Greek symbol rho (ρ).
The mean density of fluids can be useful since fluids (liquids and gases) conform to the shape of their containers. This is why it is possible to use the mean density of a substance and the dimensions of its container to estimate the weight/mass of the substance in the container.
