Torispherical Head Volume
Tags | |
UUID | 4c78b001-214e-11e8-abb7-bc764e2038f2 |
The Volume of an Torispherical Head calculator computes the volume of an torispherical head (dish-head) based on the crown radius (R), knuckle radius (a) and the height (h).
INSTRUCTIONS: Choose units and enter the following:
- (R) Crown Radius
- (a) Knuckle Radius
- (h) Height of the Head
Volume of an Torispherical Head (V): The volume is returned in cubic centi-meters and the diameter is also returned in meters. However, these can be automatically converted to compatible units via the pull-down menu. The diameter of the head is also returned. The head height, knuckle radius and diameter are related.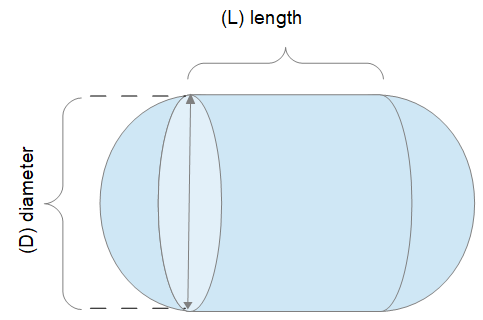 
Cylindrical Tank with Torispherical Heads If you prefer to use the diameter and knuckle radius as inputs instead of head height, use the Volume and Head Height of a Torispherical Head calculator.
The Math / Science
The formula for the volume of an Torispherical Head is as follows:
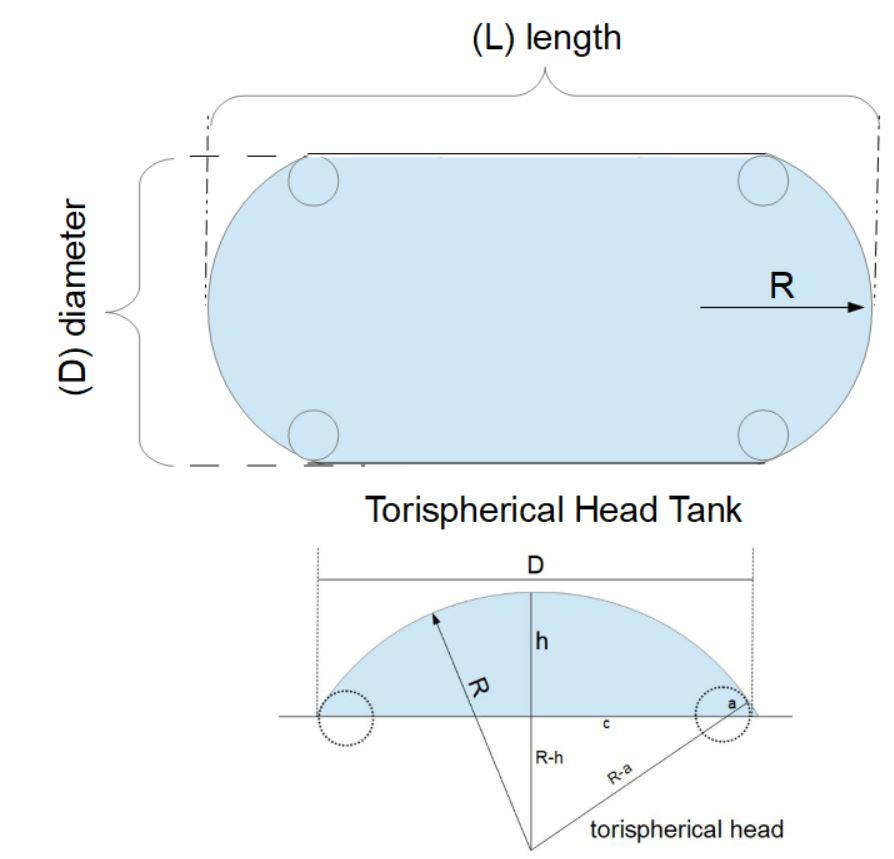
`V = π/3[2⋅h⋅R²-(2a² + c² + 2aR)(R-h)+3a²c sin‾¹( (R-h)/(R-a))]`
where:
- V is the volume of the Torispherical Head
- R is the crown radius
- h is the head height.
- a is the knuckle radius
- c is a computed length (see below)
The value of c is computed from R, h and a as follows:
`c = sqrt( (R-a)² - (R-h)² )`
The Diameter (D) is simply:
D = 2(c+a)
Torispheric-head or Dished End Calculators
Capacity of a Dished End Tank: Computes the volume of a cylindrical tank with torispherical heads based on the length and diameter of the tank and the crown radius and knuckle radius of the torispherical heads.- Torispherical Head Volume: Computes the volume and diameter of an torispherical head (dish-head) based on the crown radius, knuckle radius and the height.
- Torispherical Head Volume and Height: computes the volume of an torispherical head based on the crown radius, knuckle radius and the Diameter. It also computes the head height.
- Volume of a Torispherical Head Cylindrical Tank: Computes the volume of a cylindrical tank with torispherical heads (dish end) based on the length and diameter of the tank and the crown radius and knuckle radius of the torispherical heads.
- Mass of the Contents of Torispherical Head Tank: Computes the weight / mass of the contents of tank with torispherical heads based on the volume and density of the contents.
Storage Tank Calculators:
- Storage Capacity of a Rectangular Tank
- Above Ground Storage Tank Capacity
- Storage Capacity of a Horizontal Cylindrical Tank
- Fuel in a 268 Gallon Tank
- Fuel in a 322 Gallon Tank
- Fuel in a 150 Gallon Circular Tank
- Fuel in a 270 Gallon Circular Tank
- Fuel in a 525 Gallon Circular Tank
- Fuel in a Skid Tank
- Fuel in a 300 Gallon Skid Tank
- Fuel in a 550 Gallon Skid Tank
- Fuel in a 1000 Gallon Skid Tank
- Fuel in a 1500 Gallon Skid Tank
- Fuel in a 2000 Gallon Skid Tank
- Fuel in a 2500 Gallon Skid Tank
- Volume of a Torispherical Head
- Volume of a Torispherical Tank
- Hand Pump Volume: Computes the number of cycles (pumps or cranks) needed to move a specified volume
- Volume from Pump Rate over Time: Computes gallons pumped or consumed based on a rate and time duration.
- Comments
- Attachments
- Stats
You cannot fix all three values, ie, Crown Radius (R), Knuckle Radius (a) and Head Height (h) as they are dependent on each other.
For example, R = 1000 and a = 100, then h = R - SQRT((R-a)^2)-(((D/2)-a)^2)) = 193.774 where D is the cylinder diameter
Obviously if you worked out the exact value of H before inputting it into your calculator, then all would be fine. However, that is not the point of a calculator. Better to enter any two values and let the third be calculated, checking that it is within allowable dimensional limits, and then work out the volume.
I used the ASME VIII, Div 2 dimensional limits for Torispherical Heads of 0.7<=(R/D)<=1.0 and (a/D)>=0.06
Regards,
Peter Kemp
|
There was an error introduced when the default units were switched to millimeters. This has been resolved as of 30 July 2024.
|