The Ballistic Flight Parabolic Equation calculator computes the parabolic equation coefficients based on the launch angle above the horizon (θ) at an initial velocity (V) assuming a constant downward acceleration (g).
INSTRUCTIONS: Choose units and enter the following:
- (V) Initial Launch Velocity
- (θ) Launch Angle above the horizon.
- (h) Initial Height above the Plane
- (g) Acceleration due to gravity (default is 9.80665 m/s2)
Parabolic Flight Equation: The calculator returns the equation of the parabola to match the flight.
The Math / Science
The formula for the parabolic flight equation is:
y = a•x² + b•x + c
where:
- a = -4 • M / R²
- b = 4 • M / R
- c = h (initial height)
- M is the Ballistic Maximum Altitude without h
- R is the Ballistic Maximum Range without h
The addition of the initial height (h) to the Max Altitude and Range have the effect of shifting the parabola to the right, when all that is wanted is a shift up.
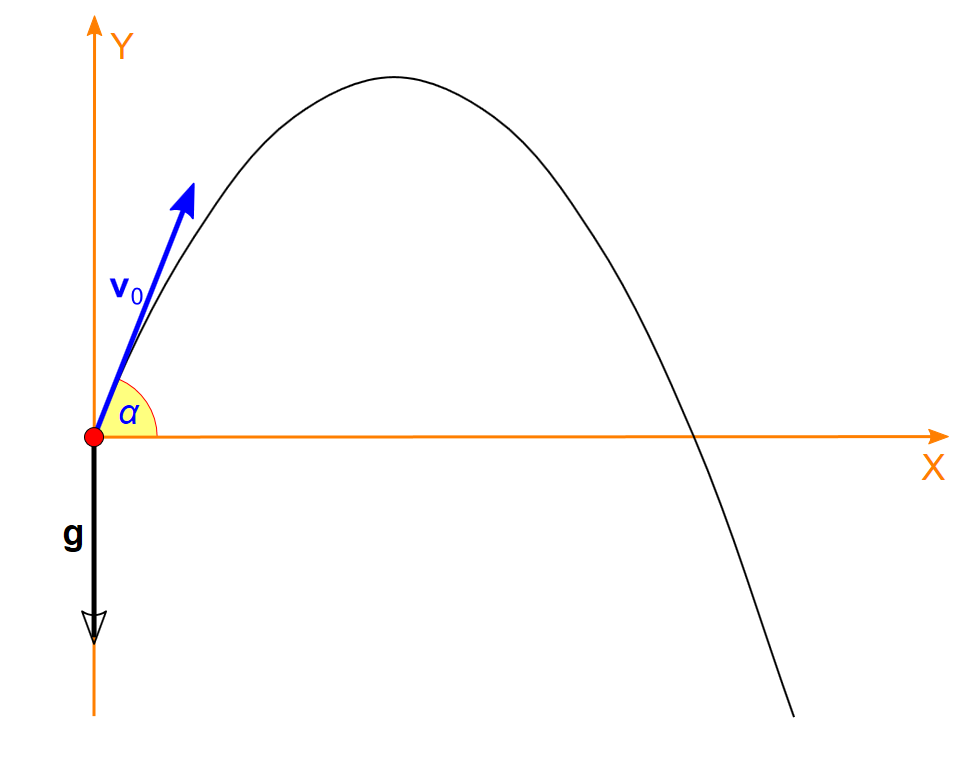
One of the most common representations of a parabola in nature is an object moving in the gravitational field of a massive body, such as the projectile motion of a body affected by the Earth's gravity. The figure shows the parabolic trajectory typifying a projectile that is affected solely by gravity, g.
Ballistic Flight Calculators:
- Ballistic Maximum Altitude: This is the maximum altitude achieved in free ballistic flight.
- Ballistic Maximum Range: This is the maximum horizontal range.
- Ballistic Flight Time: This is the time duration of free flight.
- Simplified Ballistic Range: This is the range with no initial elevation above the plane.
- Ballistic Vertical Velocity: This is the vertical velocity at a given time.
- Ballistic Horizontal Velocity: This is horizontal velocity or ground speed.
- Vertical Position (Y) in Ballistic Flight: This compute the vertical position (y) at a given time within ballistic flight.
- Horizontal Position (X) in Ballistic Flight: This compute the horizontal position (x) at a given time within ballistic flight..
- Ballistic Position at Time (t): This compute the position (x,y) at a given time within ballistic flight, where x is distance down range and y is the height above the plane.
- Ballistic Parabolic Equation provides the parabolic flight position equation based on the launch speed, height and angle.
- Acceleration Due to Gravity at Sea Level
- Velocity to achieve a Max Ballistic Height: This computes the initial velocity required to achieve the max height.
- International Gravity Equation
- Force of Earth's Gravity
- Force of Drag
Parabola Calculators
- Parabola Formula: This computes the y coordinate of a parabola in the form y = a•x²+b•x+c
- Parabolic Area: This computes the area within a section of a parabola
- Parabolic Area (Concave): This computes the outer area of a section of a parabola.
- Parabolic Arc Length: This computes the length a long a segment of a parabola.
- Paraboloid Volume: This is the volume of a parabola rotated around an axis (i.e. paraboloid)
- Paraboloid Surface Area : This is the surface area of a paraboloid.
- Paraboloid Weight: This is the weight or mass of a paraboloid.
- Ballistic Flight Parabolic Equation: This provides the formula of the parabola that matches a ballistic flight.
References
[Figure] Initial velocity of parabolic throwing
Source: Wikipedia / Fizped (modified to include motion equation)
URL: http://en.wikipedia.org/wiki/Projectile_motion#mediaviewer/File:Ferde_hajitas1.svg