Tags | |
The Ballistic Travel Time calculator computes the a amount of time an object is in free flight based on height (h) above the horizon of the launch point, initial velocity (V) of the object, and angle of launch (θ), and the vertical acceleration 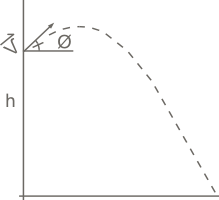(g). 
Ballistic flight
INSTRUCTIONS: Choose units and enter the following:
- (h) Initial Height above the plain
- (V) Initial Velocity of object launched (e.g. muzzle velocity from the gun or cannon)
- (θ) Launch Angle above horizon.
- (g) Acceleration due to gravity with a default of 9.80665 m/s2
Ballistic Travel Time (t): The calculator returns the time of flight (t) in seconds. However, this can be automatically converted to other time/duration units (e.g. minutes) via the pull-down menu.
The Math / Science
The formula for the ballistic travel time is:
t=Vsinθ
where:
- t is the total ballistic flight travel time
- V is the initial velocity
- θ is the launch angle
- h is the height above the plain
- g is the acceleration due to gravity
This equation calculates the time an object is in free flight based on initial parameters and downward acceleration. The initial parameters are the launch elevation or height (h) above the plane, the launch angle (theta), the initial velocity (V) and the acceleration due to gravity. A default is provided for the acceleration due to gravity of 9.8 m/s2 which is mean acceleration (at all latitudes) for sea level on Earth.
The Ballistic Flight Time equation calculates the time of flight of an object in free flight. It only takes into account the initial velocity and launch angle (also knows as the loft) and the effects of gravity through an acceleration towards the ground. This formula does not take into account other factors such as drag (see below). A default is provided for the acceleration due to gravity of 9.80665 m/s2 which is mean acceleration (at all latitudes) for sea level on Earth.
Acceleration Due to gravity
The force of gravity pulls masses towards each other. In the case of small objects (e.g. you, an arrow or the Space Shuttle) verses planetary objects (e.g. the Earth or Moon), the difference in masses result in a negligible acceleration of the large object toward the small and small object accelerating toward the center of mass of the large object. Acceleration due to gravity changes based on the mass of the object (e.g. the Earth 9.8 m/s2 verses the moon1.6 m/s2) and the distance from the center of mass. For example, since the Earth is not a perfect sphere, and more closely represented as an oblate spheroid, acceleration due to Earth gravity as Sea Level is more accurately calculated based on latitude. The international gravity formula provides an acceleration due to gravity based on latitude.
Ballistic Flight Calculators:
- Ballistic Maximum Altitude: This is the maximum altitude achieved in free ballistic flight.
- Ballistic Maximum Range: This is the maximum horizontal range.
- Ballistic Flight Time: This is the time duration of free flight.
- Simplified Ballistic Range: This is the range with no initial elevation above the plane.
- Ballistic Vertical Velocity: This is the vertical velocity at a given time.
- Ballistic Horizontal Velocity: This is horizontal velocity or ground speed.
- Vertical Position (Y) in Ballistic Flight: This compute the vertical position (y) at a given time within ballistic flight.
- Horizontal Position (X) in Ballistic Flight: This compute the horizontal position (x) at a given time within ballistic flight..
- Ballistic Position at Time (t): This compute the position (x,y) at a given time within ballistic flight, where x is distance down range and y is the height above the plane.
- Ballistic Parabolic Equation provides the parabolic flight position equation based on the launch speed, height and angle.
- Acceleration Due to Gravity at Sea Level
- Velocity to achieve a Max Ballistic Height: This computes the initial velocity required to achieve the max height.
- International Gravity Equation
- Force of Earth's Gravity
- Force of Drag
