The Simplified Range equation, R = (2v2/g) sin(Θ) cos(Θ), computes the ballistic range (horizontal displacement) of an object in free flight ignoring factors such as wind resistance. The formula is simplified because it assumes the object is launched on the plane upon which it will fall. 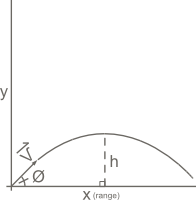
INSTRUCTIONS: Choose units and enter the following:
- (v) Initial Velocity
- (Θ) Launch Angle
- (g) Acceleration Due to Gravity (9.8 m/s2 default - Earth's surface)
Ballistic Range (R): The calculator returns the range in meters. However, this can be automatically converted into other length units via the pull-down menu.
The Math / Science
Note: this formula does not take into account any drag or other forces besides gravity, and assumes the launch point is on the plane. g is set to the appropriate constant value for acceleration due to gravity on earth in either m/s2 or ft/s2.
The formula used in this calculator is:
`R = (2*V^2)/g * sin(theta) * cos(theta) = V^2/g * sin(2theta)`
where:
- R = ballistic range
- V = initial velocity of projectile
- g = acceleration due to gravity
- θ = launch angle above the plane
Because of the trig identity, sin(2x) = 2 sin(x)cos(x), this formula will also appear in the following format: R = V2* sin(2 *Θ) / g
Ballistic Flight Calculators:
- Ballistic Maximum Altitude: This is the maximum altitude achieved in free ballistic flight.
- Ballistic Maximum Range: This is the maximum horizontal range.
- Ballistic Flight Time: This is the time duration of free flight.
- Simplified Ballistic Range: This is the range with no initial elevation above the plane.
- Ballistic Vertical Velocity: This is the vertical velocity at a given time.
- Ballistic Horizontal Velocity: This is horizontal velocity or ground speed.
- Vertical Position (Y) in Ballistic Flight: This compute the vertical position (y) at a given time within ballistic flight.
- Horizontal Position (X) in Ballistic Flight: This compute the horizontal position (x) at a given time within ballistic flight..
- Ballistic Position at Time (t): This compute the position (x,y) at a given time within ballistic flight, where x is distance down range and y is the height above the plane.
- Ballistic Parabolic Equation provides the parabolic flight position equation based on the launch speed, height and angle.
- Acceleration Due to Gravity at Sea Level
- Velocity to achieve a Max Ballistic Height: This computes the initial velocity required to achieve the max height.
- International Gravity Equation
- Force of Earth's Gravity
- Force of Drag