Standard Deviation of Mean

Processing...

The Standard Deviation of Mean (SDOM) calculator computes the standard deviation of the mean(σ_M) based on the standard deviation (σ) and the number of samples (N):

INSTRUCTIONS: Enter the following:

(σ) Standard deviation
(N) Number of samples

Standard Deviation of the Mean (SDOM): The calculator returns the standard deviation of the mean(σ_M).

The Math / Science

The standard deviation of the mean (SDOM) is sometimes also known as the standard error of the mean (SEM). This quantity is useful in that it helps quantify the uncertainty in the estimate of the mean.

The formula for the Standard Deviation of Mean (SDOM) is:

`s_m = s/(sqrtN)`

where:

s_m is the standard deviation of mean (SDOM)
s is the standard deviation
N is the number of samples

To compute the standard deviation and sample size, use the Simple Stats Calculator [CLICK HERE]to enter your data and see the observational statistics which include both the standard deviation and number of samples.

Key Points about SEM:

Interpretation: The SEM gives an estimate of how far the sample mean is likely to be from the population mean. A smaller SEM indicates that the sample mean is a more precise estimate of the population mean.
Relationship with Sample Size: The SEM decreases as the sample size increases, reflecting that larger samples tend to provide more accurate estimates of the population mean.
Usage: The SEM is commonly used in hypothesis testing and confidence intervals to assess the reliability of the sample mean as an estimate of the population mean.

In summary, the standard error of the mean (SEM) is a measure of the dispersion of sample means around the population mean and is crucial for understanding the accuracy of the sample mean as an estimate of the true population mean.

Estimated Statistics

Statistics Calculators

Observational Stats: This function accepts a table (rows and columns separated by commas) of numbers and calculates observational statistics for any of the columns. This includes count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
Simple Stats: This is also provides a full set of observational stats, but on a single row of numbers separated by commas. The observational stats include count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
Frequency Distribution: This function lets you enter a string of numbers separated by commas, a low and high range and a number of bins. It then computes how many of the observations are in each of the bins between the high and low values designated.
Paired Sample t-test: This computes the various parameters associated with the Paired Sample t-test.
ANOVA (one way): The computes the F Score and details for one way analysis of variance for a nxm matrix of observations.
(χ²) Chi-Square Test: This computes the Chi-Square value for an nxm array of data and provides the degrees of freedom.
Linear Regression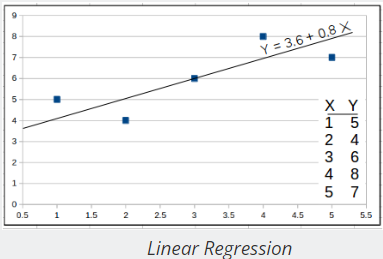: This computes the regression line (least-squares) through a set of X and Y observations. It also computes the regression coefficient (r).
Least-squares Trend Inference : This is a linear equation used with Linear Regression to compute a predicted value of Y based on X.
Wilcoxon Signed Rank Test: This provides the Wilcoxon statistics and critical value for two groups of numeric observations based on an alpha value and whether it's a one or two tailed test.
Slope-Intercept form of a Line: This provides the slope intercept form (y = mx+b) of a line based on two coordinates.
Slope between two points: This provides the slope between two coordinates.
Linear Equation: This computes the range (y) of a linear equation (y = mx +b) and includes a graphing function.
Probability between z SCORES: 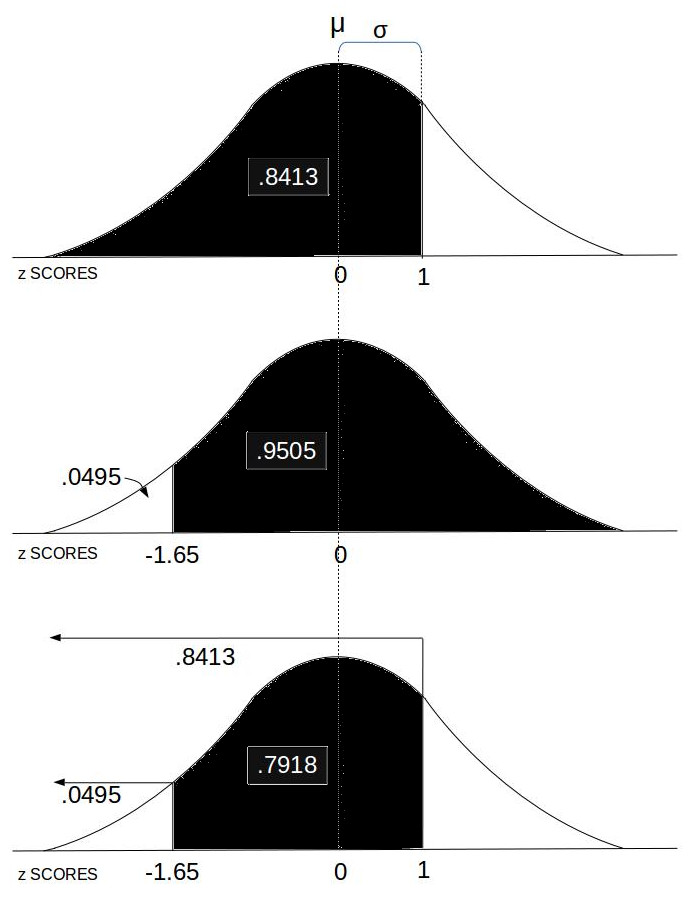This computes the area under the Normal Distribution curve between two z SCOREs which equates to the probability of an event in that range.
Stats Calc: College level statistics calculator with a bundle including most of the functions in this list.
Count: This computes the number (n) of observations in a set of numbers.
Minimum: This computes the minimum (min) value in a set of numbers.
Maximum: This computes the maximum (max) value in a set of numbers.
Numeric Sort: This sorts (ascending or descending) a set of comma separated numerical observations.
Random Sample (k items): The provides a random subset of a specified size (k) in a set of comma separated numerical observations.
Random Real Number in Range: The provides a random real number between two specified real numbers (upper and lower bounds).
Radom Integer: The provides a random integer between two specified integers (upper and lower bounds).
Frequency Distribution: This provides a frequency distribution table for a comma separated set of numbers with a specified number of frequency bins between a lower and upper data range.
Sum (Σx): This is computes the sum of the values in a set.
Sum of Squares (Σx²): This computes the sum of the squared values in a set.
Sum Squared (Σx)²: This computes the square of the summed values in a set.
Mean (μ): This computes is the mean (average) of values in a set.
Median: This identifies the middle ordered value in a set of numbers.
Statistical Mode: This identifies the most recurring observation in a set of numbers.
Mid Point: This is identifies the mid point of the observation range in a set of numbers.
Range: This is computes the difference between the max and the min values in a set of number.
Population Variance (σ²): This computes the variance, a metric regarding the spread of values, for a population set of numeric values.
Population Standard Deviation (σ): This computes the standard deviation for a population set of numeric values.
Sample Variance (s²) : This computes the variance, a metric regarding the spread of values, for a sample set of numeric values within a greater population.
Sample Standard Deviation (s): This computes the standard deviation for a sample set of numeric values within a greater population.
z SCORE Formula: This computes the z SCORE for a value base on the mean and standard deviation.
z SCORE: This computes the z SCORE for a value (Raw Score) based on a set of values, and whether that set is sample or population.
Percentile: This computes the percentile of a value (y) in a set (X) of values.
Standard Deviation of Mean (SDOM): This computes the standard deviation of mean, sometimes also known as the standard error of the mean (SEM), useful to helps quantify the uncertainty in the estimate of the mean.
Percent Relative Standard Deviation (%RSD): This computes the percent relative standard deviation, also known as the coefficient of variation (CV). The %RSD is a measure of the dispersion of a probability distribution.