Observational Statistics

Processing...

The Observational Statistics calculator computes the most common observational statistics for columns in a table of data.

INSTRUCTIONS: Enter the following:

(x) Numeric Observations. Enter rows of comma separated numeric values e.g. 4,-1.2,8,9 . To do so, click on the field and
1. enter the data manual, or
2. use cut / copy / paste, or
3. upload a csv with a uniform table of real numbers.
(c) Column Number.

STATISTICS: The calculator returns the descriptive statistics below for the identified column.

count - number (n) of values in the column.
min - minimum value
max - maximum value
sum(Σx) - sum of the values in a set.
Σx² - sum of the squared values
(Σx)² - square of the summed values.
mean - mean (average) of values
median - middle ordered value
mid point - mid point of value range
mode - most frequent observation
range - difference between the max and the min.
MAD - Mean Absolute Deviation
SDOM - Standard Deviation of Mean
sort up - values in ascending order.
sort down - values in descending order.
var-pop - population variance of the values
sd-pop - population standard deviation of the values
var-sample - sample variance of the values
sd-sample - sample standard deviation of the values

How to Enter Data

Enter the data in comma separated values with a new line for each record. Note: it is important to be consistent with number of columns when manually entering the data.

One can also upload a CSV (comma separated values) file from your device into this calculator by clicking on the

. button.

Example

Enter the following tabular data and choose a column between 1 and 4:

-56,347,356,147
326,-116,386,-276
23,309,-230,-109
390,49,385,405
-87,289,32,33
-210,382,244,5
-85,206,386,44
318,-294,-16,-294
357,-152,-154,147
482,-16,-241,-191
-85,281,267,280
254,364,352,72
-32,-322,-90,-385
460,434,-89,461
23,49,-243,-42
128,-228,-137,-61
370,-75,32,-287
306,-387,51,33
-23,-282,467,271

You will see the observational statistics for that column.

This calculator is a prominent feature with other statistical functions in the College Level Statistics Calculator (Stat Calc).

Statistics Calculators

Observational Stats: This function accepts a table (rows and columns separated by commas) of numbers and calculates observational statistics for any of the columns. This includes count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
Simple Stats: This is also provides a full set of observational stats, but on a single row of numbers separated by commas. The observational stats include count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
Frequency Distribution: This function lets you enter a string of numbers separated by commas, a low and high range and a number of bins. It then computes how many of the observations are in each of the bins between the high and low values designated.
Paired Sample t-test: This computes the various parameters associated with the Paired Sample t-test.
ANOVA (one way): The computes the F Score and details for one way analysis of variance for a nxm matrix of observations.
(χ²) Chi-Square Test: This computes the Chi-Square value for an nxm array of data and provides the degrees of freedom.
Linear Regression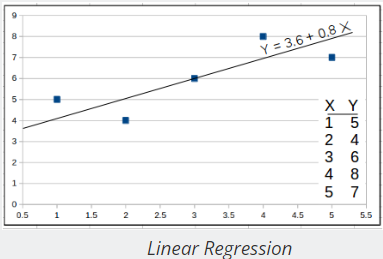: This computes the regression line (least-squares) through a set of X and Y observations. It also computes the regression coefficient (r).
Least-squares Trend Inference : This is a linear equation used with Linear Regression to compute a predicted value of Y based on X.
Wilcoxon Signed Rank Test: This provides the Wilcoxon statistics and critical value for two groups of numeric observations based on an alpha value and whether it's a one or two tailed test.
Slope-Intercept form of a Line: This provides the slope intercept form (y = mx+b) of a line based on two coordinates.
Slope between two points: This provides the slope between two coordinates.
Linear Equation: This computes the range (y) of a linear equation (y = mx +b) and includes a graphing function.
Probability between z SCORES: 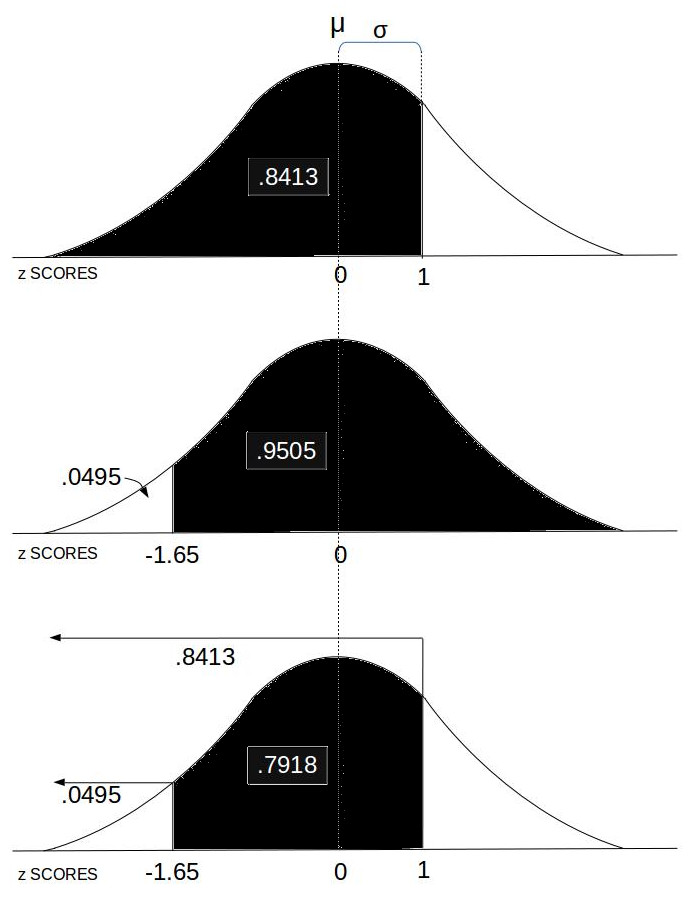This computes the area under the Normal Distribution curve between two z SCOREs which equates to the probability of an event in that range.
Stats Calc: College level statistics calculator with a bundle including most of the functions in this list.
Count: This computes the number (n) of observations in a set of numbers.
Minimum: This computes the minimum (min) value in a set of numbers.
Maximum: This computes the maximum (max) value in a set of numbers.
Numeric Sort: This sorts (ascending or descending) a set of comma separated numerical observations.
Random Sample (k items): The provides a random subset of a specified size (k) in a set of comma separated numerical observations.
Random Real Number in Range: The provides a random real number between two specified real numbers (upper and lower bounds).
Radom Integer: The provides a random integer between two specified integers (upper and lower bounds).
Frequency Distribution: This provides a frequency distribution table for a comma separated set of numbers with a specified number of frequency bins between a lower and upper data range.
Sum (Σx): This is computes the sum of the values in a set.
Sum of Squares (Σx²): This computes the sum of the squared values in a set.
Sum Squared (Σx)²: This computes the square of the summed values in a set.
Mean (μ): This computes is the mean (average) of values in a set.
Median: This identifies the middle ordered value in a set of numbers.
Statistical Mode: This identifies the most recurring observation in a set of numbers.
Mid Point: This is identifies the mid point of the observation range in a set of numbers.
Range: This is computes the difference between the max and the min values in a set of number.
Population Variance (σ²): This computes the variance, a metric regarding the spread of values, for a population set of numeric values.
Population Standard Deviation (σ): This computes the standard deviation for a population set of numeric values.
Sample Variance (s²) : This computes the variance, a metric regarding the spread of values, for a sample set of numeric values within a greater population.
Sample Standard Deviation (s): This computes the standard deviation for a sample set of numeric values within a greater population.
z SCORE Formula: This computes the z SCORE for a value base on the mean and standard deviation.
z SCORE: This computes the z SCORE for a value (Raw Score) based on a set of values, and whether that set is sample or population.
Percentile: This computes the percentile of a value (y) in a set (X) of values.
Standard Deviation of Mean (SDOM): This computes the standard deviation of mean, sometimes also known as the standard error of the mean (SEM), useful to helps quantify the uncertainty in the estimate of the mean.
Percent Relative Standard Deviation (%RSD): This computes the percent relative standard deviation, also known as the coefficient of variation (CV). The %RSD is a measure of the dispersion of a probability distribution.

Thanks to Dr. Lee Hammerstrom, professor of math stats at Eastern Nazarene College, for his advice and testing.

The Math

The formulas for the statistics are as follows:

sum

`S = sum(x)`

sum of squares

Σx²`= sum(x^2)`

square of the sum

(Σx)² = `(sum(x))^2`

averages

mean: `mu = (sum(x))/n` where n is the number of observations
median: middle value if in an odd number of observations. If there is an even number of observations, it's the average of the two middle values.
mid-point: `mp = (min + max)/2`

variance

Population Variance: `sigma^2 = (sum_1^n(x_n-mu)^2)/n`
Sample Variance: `sigma^2 = (sum_1^n(x_n-mu)^2)/(n-1)`

standard deviation

Population Standard Deviation: `sigma = sqrt((sum_1^n(x_n-mu)^2)/n)`
Sample Standard Deviation: `sigma = sqrt((sum_1^n(x_n-mu)^2)/(n-1))`

Mean Absolute Deviation

MAD = `1/n sum_(i=1)^n | x_i - barx |`

Statistics Calculators

Stats Calc - Complete set of entry level college statistics functions
Simple Stats - Complete set of Observational statistics for a set of data
Linear Regression - Least-squares trend line for a set of data
One Way ANOVA - One way Analysis of Variance for three sets of data

Growth Calculators

Logistic Growth
Malthusian Growth Model
Organism Count (Logistic Growth)
Max Potential Growth Rate (biotic potential)
How Many Ancestors
Simple Stats Calc - Simple observation statistics (see below)
Math Statistics Calc - College level statistics and regression calculator.

Statistics in Culture

"There are three kinds of lies: lies, damn lies and statistics." Mark Twain