The Statistics Calculator provides college level statistics functionality.    Frequency Distribution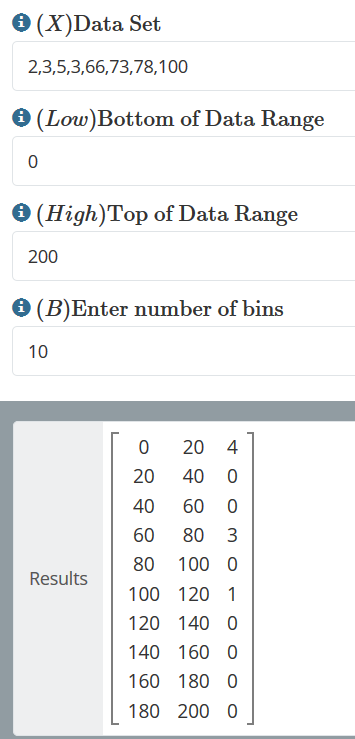This includes observation stats (min, max, mean, median, population and sample variance and standard deviation), sort, random sample, t-test, linear regression and more.  See the following:

• Observational Stats:  This function accepts a table of numbers separated by commas and calculates observational statistics for any of the columns.  This includes count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
• Frequency Distribution:  This function lets you enter a string of numbers separated by commas, a low and high range and a number of bins.  It then computes how many of the observations are in each of the bins between the high and low values designated. 
• Random Sample (k):  This generate a random sample of k items within a set.
• Percentile:  This computes the relative percentile of an observation verses a set.
• P(A) = F / T: This computes the probability of a favorable event in a total number of outcomes.
• P(n,S) - Binomial Probability:  Probability of S successes in n trials of a binomial distribution.
• B_C: - The binomial coefficient derived from Pascal's Triangle. 
• zSCORE (y in X):  This computes the z SCORE of an observation in a set (X). 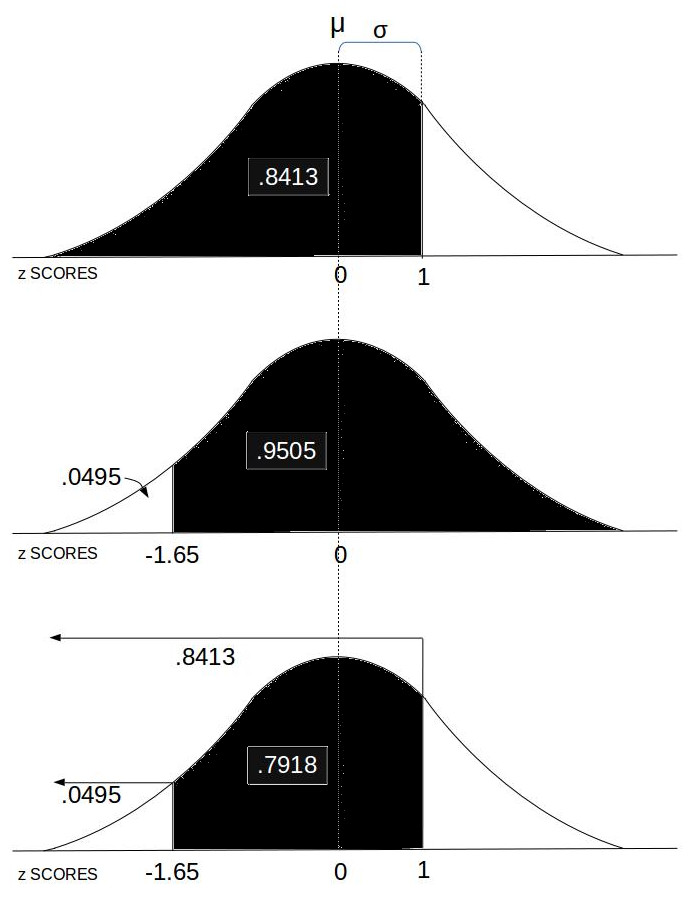  Normal Distribution and z SCORES
• zSCORE (y,μ,σ):  This computes the z SCORE of an observation based on the mean and standard deviation.
• z from P(y):  This computes the z SCORE based on a probability or percentile in a Normal Distribution table.
• P(y) left of z: This computes the percentile, probability or area under the curve of a Normal Distribution left of the z SCORE.
• P(y) right of z: This computes the percentile, probability or area under the curve of a Normal Distribution right of the z SCORE.
• Probability between z SCORE:  This computes the area under the Normal Distribution curve between z SCOREs.
• Raw Score (P,μ,σ): This computes the raw score associated with a percentile in a Normal Distribution (μ,σ).
• Paired Sample t-test:  This computes the various parameters associated with the Paired Sample t-test.
• y = a + bx:  This is linear equation used with Linear Regression to predict values of Y.
• ANOVA (one way): The is one way analysis of variance
• (χ²) Chi-Square Test: This computes the Chi-Square value for an nxm array of data and provides the degrees of freedom.
• Linear Regression:  This computes the regression line (least-squares) through a set of X and Y observations.  It also computes the regression coefficient (r). 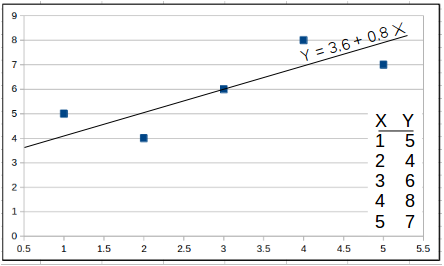             Linear Regression

How to Enter Data

The functions in this calculator accept comma separated values.  If the data has one dimension, it can be entered via one row of comma separated values such as this:

3.2,6.3,9.1.23.14.33,77.16,-99.2,-73.5

If the data has multiple dimensions and is in table form, the functions accept comma separated rows of values.  For example, one could enter the following information in two columns.  It matches the Linear Regression data shown in the graphic.

One could also upload the same data from a .CSV text file in the same format.

The Math / Science

The formulas for the statistics are as follows:

sum

     `S = sum_1^n(x)`

square of the sum

      (Σx)² = S²

sum of squares (Σx²)

      Σx² = `sum_1^n(x^2)`

averages

• mean:     `mu = (sum(x))/n`  where n is the number of observations
• median:  middle value if in an odd number of observations.  If there is an even number of observations, it's the average of the two middle values.
• mode:  the most repeated observation.
• mid-point:  `mp = (min + max)/2`

variance

• Population Variance: `sigma^2 = (sum_1^n(x_n-mu)^2)/n`
• Sample Variance:       `sigma^2 = (sum_1^n(x_n-mu)^2)/(n-1)`

standard deviation

• Population Standard Deviation:   `sigma = sqrt((sum_1^n(x_n-mu)^2)/n)`
• Sample Standard Deviation:         `sigma = sqrt((sum_1^n(x_n-mu)^2)/(n-1))`

Permutations

• Permutations:                                _nP_r = ` (n!)/((n-r)!)`
• Circular Permutations:                 P_c(n,r) = ` (n!)/(r(n-r)!)`
• Permutations with repetitions:   P_r(n) = n^r

Combinations

• Combinations:                                    _nC_k= ` (n!)/(k!(n-k)!)`
• Combinations with repetitions:      C_r(n, k) = ` ((n+k-1)!)/(k!(n-1)!)`

z SCORE

The formula for the z SCORE is as follows:

     `z_y =   (y - μ_X)/s`   where:

        - y is the single observation
        - μ is the mean
        - s is the sample or population standard deviation.

Least-squares Linear Regression

The formula for the least-squared regression line is in the following form:   y = a + bx

                      where:  `b = (  (sum(XY) - (sumX * sumY)"/n")) / (sum(X^2) - (sumX)^2"/n") `

                          and:  ` a = MY - b*MX`           MY is mean of Y.  MX is mean of X.

---

Statistics Calculators

• Observational Stats:  This function accepts a table (rows and columns separated by commas) of numbers and calculates observational statistics for any of the columns.  This includes count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
• Simple Stats: This is also provides a full set of observational stats, but on a single row of numbers separated by commas. The observational stats include count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
• Frequency Distribution:  This function lets you enter a string of numbers separated by commas, a low and high range and a number of bins.  It then computes how many of the observations are in each of the bins between the high and low values designated. 
• Paired Sample t-test:  This computes the various parameters associated with the Paired Sample t-test.
• ANOVA (one way): The computes the F Score and details for one way analysis of variance for a nxm matrix of observations.
• (χ²) Chi-Square Test: This computes the Chi-Square value for an nxm array of data and provides the degrees of freedom.
• Linear Regression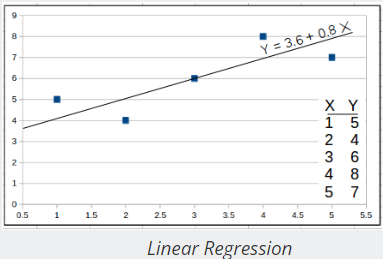:  This computes the regression line (least-squares) through a set of X and Y observations.  It also computes the regression coefficient (r).
• Least-squares Trend Inference :  This is a linear equation used with Linear Regression to compute a predicted value of Y based on X.
• Wilcoxon Signed Rank Test: This provides the Wilcoxon statistics and critical value for two groups of numeric observations based on an alpha value and whether it's a one or two tailed test.
• Slope-Intercept form of a Line: This provides the slope intercept form (y = mx+b) of a line based on two coordinates.
• Slope between two points: This provides the slope between two coordinates.
• Linear Equation: This computes the range (y) of a linear equation (y = mx +b) and includes a graphing function.
• Probability between z SCORES: 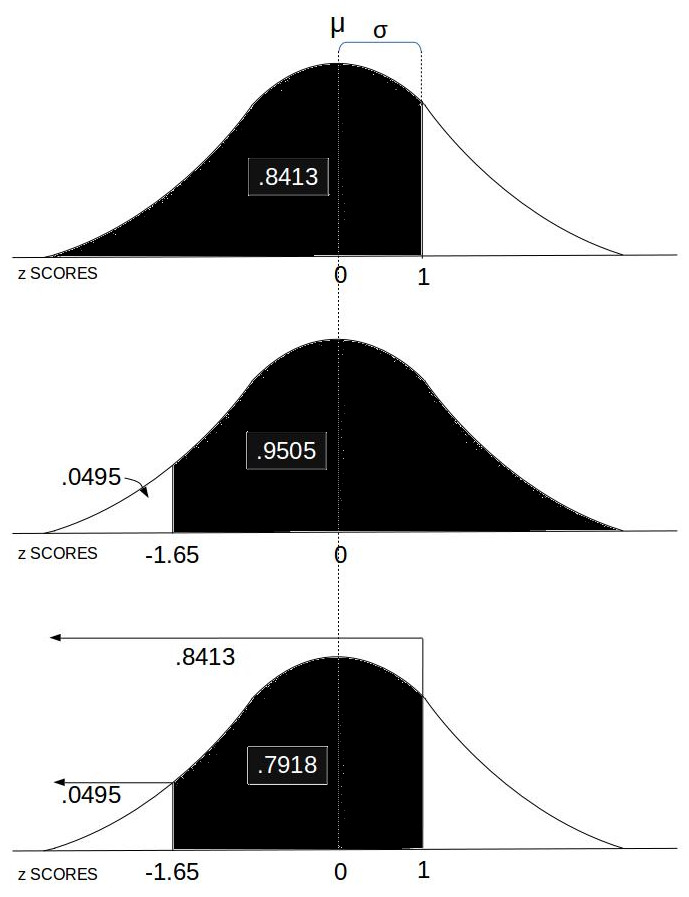This computes the area under the Normal Distribution curve between two z SCOREs which equates to the probability of an event in that range.
• Stats Calc: College level statistics calculator with a bundle including most of the functions in this list.
• Count: This computes the number (n) of observations in a set of numbers.
• Minimum: This computes the minimum (min) value in a set of numbers.
• Maximum: This computes the maximum (max) value in a set of numbers.
• Numeric Sort: This sorts (ascending or descending) a set of comma separated numerical observations.
• Random Sample (k items): The provides a random subset of a specified size (k) in a set of comma separated numerical observations.
• Random Real Number in Range: The provides a random real number between two specified real numbers (upper and lower bounds).
• Radom Integer: The provides a random integer between two specified integers (upper and lower bounds).
• Frequency Distribution: This provides a frequency distribution table for a comma separated set of numbers with a specified number of frequency bins between a lower and upper data range. 
• Sum (Σx): This is computes the sum of the values in a set.
• Sum of Squares (Σx²): This computes the sum of the squared values in a set.
• Sum Squared (Σx)²:  This computes the square of the summed values in a set.
• Mean (μ): This computes is the mean (average) of values in a set.
• Median: This identifies the middle ordered value in a set of numbers.
• Statistical Mode: This identifies the most recurring observation in a set of numbers.
• Mid Point: This is identifies the mid point of the observation range in a set of numbers.
• Range: This is computes the difference between the max and the min values in a set of number.
• Population Variance (σ²): This computes the variance, a metric regarding the spread of values, for a population set of numeric values.
• Population Standard Deviation (σ):  This computes the standard deviation for a population set of numeric values.
• Sample Variance (s²) : This computes the variance, a metric regarding the spread of values, for a sample set of numeric values within a greater population.
• Sample Standard Deviation (s): This computes the standard deviation for a sample set of numeric values within a greater population.
• z SCORE Formula: This computes the z SCORE for a value base on the mean and standard deviation.
• z SCORE: This computes the z SCORE for a value (Raw Score) based on a set of values, and whether that set is sample or population. 
• Percentile: This computes the percentile of a value (y) in a set (X) of values.
• Standard Deviation of Mean (SDOM):  This computes the standard deviation of mean, sometimes also known as the standard error of the mean (SEM), useful to helps quantify the uncertainty in the estimate of the mean.  
• Percent Relative Standard Deviation (%RSD): This computes the percent relative standard deviation, also known as the coefficient of variation (CV).  The %RSD is a measure of the dispersion of a probability distribution.

---

Economics Calculators

• Average Total Cost
• Basic Price Elasticity of Demand.
• Midpoint Method of Price Elasticity of Demand
• Midpoint Method of Price Elasticity of Demand with automatic Quantity Unit Handling:
  • Price Elasticity of Demand (Volume Units)
  • Price Elasticity of Demand (Area Units)
  • Price Elasticity of Demand (Weight or Mass Units)
  • Price Elasticity of Demand (Length Units)
• Cobb Douglas Utility Maximizing Consumption Bundle
• Statistics Calculator
• Price and Unit Comparison Shopping Calculator
• Production and Consumption Rate Calculator

---

Growth Calculators

• Logistic Growth
• Malthusian Growth Model
• Organism Count (Logistic Growth)
• Max Potential Growth Rate (biotic potential)
• How Many Ancestors
• Simple Stats Calc - Simple observation statistics (see below)
• Math Statistics Calc - College level statistics and regression calculator.

Thanks

Thanks to Dr. Richard (Rich) D. Platt, Associate Professor of Psychology at St Mary's College of Maryland, for his advice and testing.  Special thanks to Ms. Caroline Robertson for getting this library of equations off the ground.